题目内容
16.已知数列{an},{bn}的各项均为正数,且对任意n∈N*,都有bn,an,bn+1成等差数列.an,bn+1,an+1成等比数列,且b1=6,b2=12.(I)求证数列$\left\{{\sqrt{a_n}}\right\}$是等差数列,并求an;
(Ⅱ)设Tn=$\frac{{2}^{\sqrt{{a}_{1}}}•{b}_{1}}{2}+\frac{{2}^{\sqrt{{a}_{2}}}•{b}_{2}}{3}+…+\frac{{2}^{\sqrt{{a}_{n}}}•{b}_{n}}{n+1}$,求Tn.
分析 (I)由等差数列和等比数列的性质,结合等差数列的中项,即可证明数列$\left\{{\sqrt{a_n}}\right\}$是等差数列,运用等差数列的通项公式,求出$\sqrt{{a}_{n}}$,可得an;
(Ⅱ)由(Ⅰ)中的结论,即可得到bn.令cn=$\frac{{2}^{\sqrt{{a}_{n}}}•{b}_{n}}{n+1}$=(n+2)•2n+2,再由错位相减法,求和即可得到.
解答 (I)证明:∵an,bn+1,an+1成等比数列,
∴bn+12=an•an+1,(n∈N*)
∴bn+1=$\sqrt{{a}_{n}{a}_{n+1}}$,
∴bn=$\sqrt{{a}_{n}{a}_{n-1}}$,(n≥2)
∵bn,an,bn+1成等差数列,
∴2an=bn+bn+1,(n∈N*)
∴2an=$\sqrt{{a}_{n}{a}_{n-1}}$+$\sqrt{{a}_{n}{a}_{n+1}}$=$\sqrt{{a}_{n}}$($\sqrt{{a}_{n+1}}$+$\sqrt{{a}_{n-1}}$),(n≥2)
2$\sqrt{{a}_{n}}$=$\sqrt{{a}_{n-1}}$+$\sqrt{{a}_{n+1}}$,(n≥2),
∴数列{$\sqrt{{a}_{n}}$}是等差数列.
∵b1=6,b2=12,
∴2a1=b1+b2=18,即a1=9,
a2=$\frac{{{b}_{2}}^{2}}{{a}_{1}}$=$\frac{1{2}^{2}}{9}$=16,
∴数列$\left\{{\sqrt{a_n}}\right\}$的公差d=$\sqrt{{a}_{2}}$-$\sqrt{{a}_{1}}$=4-3=1,
$\sqrt{{a}_{n}}$=$\sqrt{{a}_{1}}$+(n-1)d=n+2,
即有an=(n+2)2;
(Ⅱ)解:n≥2时,bn=$\sqrt{{a}_{n}{a}_{n-1}}$=$\sqrt{(n+2)^{2}(n+1)^{2}}$
=(n+1)(n+2),
又b1=6适合上式.
∴bn=(n+1)(n+2).
设cn=$\frac{{2}^{\sqrt{{a}_{n}}}•{b}_{n}}{n+1}$=$\frac{{2}^{n+2}•(n+1)(n+2)}{n+1}$
=(n+2)•2n+2,
Tn=c1+c2+…+cn=3•23+4•24+…+(n+1)•2n+1+(n+2)•2n+2,
2Tn=6•23+8•24+…+(n+1)•2n+2+(n+2)•2n+3,
两式相减可得,-Tn=24+24+25+…+2n+2-(n+2)•2n+3
=24+$\frac{16(1-{2}^{n-1})}{1-2}$-(n+2)•2n+3.
即有Tn=(n+1)•2n+3-8.
点评 本题考查等差数列的证明,考查数列的通项公式和数列求和的求法:错位相减法,是中档题,解题时要认真审题,注意构造法的合理运用.

| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
 某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: 如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π]),OP所经过的在正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论:
如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π]),OP所经过的在正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论: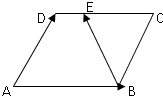 在边长为1的菱形ABCD中,∠A=60°,E是线段CD上一点,满足|$\overrightarrow{CE}$|=2||$\overrightarrow{DE}$|,如图所示,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
在边长为1的菱形ABCD中,∠A=60°,E是线段CD上一点,满足|$\overrightarrow{CE}$|=2||$\overrightarrow{DE}$|,如图所示,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.