Question

 (本小题满分12分，(Ⅰ)小问4分，(Ⅱ)小问8分.)如图，椭圆的中心为原点，离心率=,一条准线的方程是=.

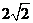(Ⅰ)求椭圆的标准方程;

(Ⅱ)设动点满足:=,其中,是椭圆上的点，直线与的斜率之积为.问:是否存在定点,使得与点到直线：=的距离之比为定值？若存在,求的坐标;若不存在,说明理由.

 

 

 

Answer 1

【答案】

 【命题意图】本题考查了椭圆标准方程的求解与椭圆的定植问题，考查学生综合运用知识解决问题能力、运算求解能力和探究问题能力，难度较大.

【解析】(Ⅰ) ∵==,=,解得=2，=，∴==2，

∴椭圆的标准方程为；

(Ⅱ)设P(，)，，，则由=，得

==，

∴=，=，

  ∵,在椭圆上，∴，，

∴==

==.

设,分别表示直线，的斜率，由题设条件知，==，

∴，  ∴=20， 

∴点在椭圆上，该椭圆的右焦点为(,0),离心率=，右准线为：=，

∴根据椭圆的第二定义，存在定点(,0)，使得与点到直线的距离之比为定值.