题目内容
曲线
在
处的切线方程是________，在x=x0处的切线与直线y=x和y轴围成三角形的面积为________．
3x+y-4=0 2
分析：求导数可得切线的斜率，代值可得点的坐标，由点斜式可得方程；写出x=x0处的切线方程，求得与直线y=x和y轴的交点坐标，进而可得面积．
解答：由题意可得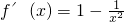
，f（
）=
故曲线在x=处的切线的斜率k=
=-3，
故切线方程为y-=-3（x-），即3x+y-4=0；
可得在x=x0处的切线斜率为
，
故方程为：y-（
）=（
）（x-x0），
令y=x可得x=y=2x0，令x=0可得y=
，
故三角形的面积为S=×
=2，
故答案为：3x+y-4=0；2
点评：本题考查利用导数研究曲线上某点的切线方程，涉及三角形面积的求解，属中档题．
分析：求导数可得切线的斜率，代值可得点的坐标，由点斜式可得方程；写出x=x0处的切线方程，求得与直线y=x和y轴的交点坐标，进而可得面积．
解答：由题意可得
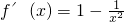，f（）=故曲线在x=
处的切线的斜率k==-3，故切线方程为y-
=-3（x-），即3x+y-4=0；可得在x=x0处的切线斜率为
，故方程为：y-（
）=（）（x-x0），令y=x可得x=y=2x0，令x=0可得y=
，故三角形的面积为S=
×=2，故答案为：3x+y-4=0；2
点评：本题考查利用导数研究曲线上某点的切线方程，涉及三角形面积的求解，属中档题．
练习册系列答案
相关题目
在
上满足 
，则曲线
在
处的切线方程是( )
B．
C．
D．
在
上满足 
，则曲线
在
处的切线方程是
B．
C．
D．
在
处的切线方程是（ ）
B．
D．
在
处的切线方程是____________．
在
处的切线方程是 (
)
(B) 
(C) 
(D) 