题目内容
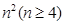 个正数排成
个正数排成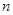 行
行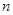 列:
列:
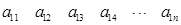
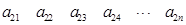
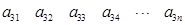
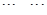
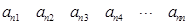
其中每一行的数由左至右成等差数列,每一列的数由上至下成等比数列,并且所有公比相等,已知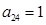 ,
,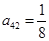 ,
,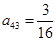 ,试求
,试求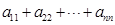 的值. (本题满分13分)
的值. (本题满分13分)
【答案】
解:设 ,第一行数的公差为
,第一行数的公差为 ,第一列数的公比为
,第一列数的公比为 ,可得
,可得
又设第一行数列公差为 ,各列数列的公比为
,各列数列的公比为 ,则第四行数列公差是
,则第四行数列公差是 ,于是可得
,于是可得
 .………………….….
(3分)
.………………….….
(3分)
解此方程组,得 ,由于给
,由于给 个数都是正数,必有
个数都是正数,必有 ,从而有
,从而有 ,
.………………………. (4分)
,
.………………………. (4分)
于是对任意的 ,有
,有 …….……
(6分)
…….……
(6分)
得 , ………………….
(8分)
, ………………….
(8分)
又
 . ………………….
(10分)
. ………………….
(10分)
两式相减后得: .
…………… (12分)
.
…………… (12分)
所以
 ………………….
(13分)
………………….
(13分)
【解析】略

练习册系列答案
相关题目
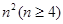 个正数排成
个正数排成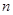 行
行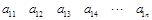
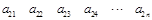
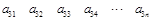
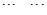
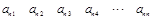
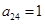 ,
,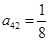 ,
,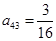 ,则
,则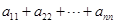 = 。
= 。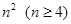 个正数排成
个正数排成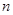 行
行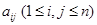 表示位于第
表示位于第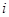 行第
行第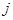 列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且每一列的数的公比都等于
列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且每一列的数的公比都等于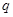 . 若
. 若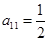 ,
,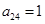 ,
,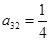 ,
则
,
则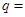 ________,
________,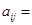 __________.
__________.
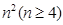 个正数排成
个正数排成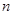 行
行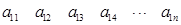
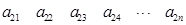
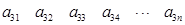
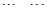
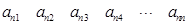
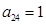 ,
,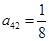 ,
,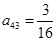 ,试求
,试求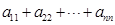 的值. (本题满分13分)
的值. (本题满分13分)