题目内容
在直三棱柱ABC—A1B1C1中,AC⊥BC,F为BB1上一点,BF=a,FB1=4a,BC=2a.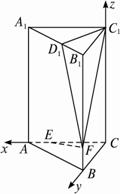
(1)若E为AC上不同于A和C的任意一点,求证:EF⊥FC1;
(2)A1B1=3a,求FC1与平面AA1B1B所成的角.
(1)证法一:如图,建立坐标系,?

则F(0,2a,a),C1(0,0,5a),?
设E(x,0,0),∴![]() =(-x,2a,a),
=(-x,2a,a),![]() =(0,-2a,4a).?
=(0,-2a,4a).?
∴![]() ·
·![]() =0.?
=0.?
∴EF⊥FC1.
证法二:设![]() =2a,
=2a,![]() =5c,
=5c,![]() =x,其中a·c=a·x=c·x=0,|a|=|c|=1,?
=x,其中a·c=a·x=c·x=0,|a|=|c|=1,?
∴![]() =-c-2a+x,?
=-c-2a+x,?
![]() =4c-2a.?
=4c-2a.?
∴![]() ·
·![]() =-4+4=0.
=-4+4=0.
∴FE⊥FC1.?
(2)解析:过C1作C1D1⊥A1B1于D1,连FD1,∴C1D1⊥面A1ABB1.?
∴∠C1FD1为所求角,C1D1⊥D1F.?
∵|A1B1|=3a,|B1C1|=2a,?
∴|A1C1|=![]() a.?
a.?
∴|D1C1|=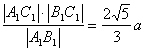 ,?
,?
![]() .?
.?
∴sin∠C1FD1=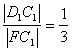 .?
.?
∴∠C1FD1=arcsin![]() .
.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
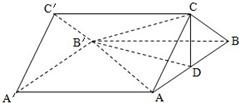 如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.
如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点. (2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a,
(2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a, 如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数). 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,