Question

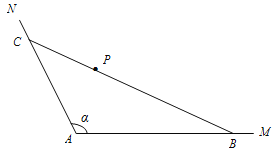
【题目】设平面内的向量 ， ， ，点P在直线OM上，且 ．
（1）求 的坐标；
（2）求∠APB的余弦值；
（3）设t∈R，求 的最小值．

Answer 1

【答案】
（1）解：∵点P在直线OM上，设

∴ ，

∴ ，解得 ，

∴ ．

（2）解： ， ，

∴

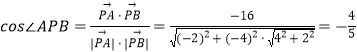
（3）解： ，

∴ =2（t﹣2）2+2．

当t=2时，（ +t ）2取得最小值2，

∴ 的最小值为 ．

【解析】（1）根据P，O，M三点共线可设 ，利用数量积公式列方程解出；（2）计算 的模长，代入向量夹角公式计算；（3）计算 2得到关于t的二次函数，求出函数的最小值即可．
【考点精析】根据题目的已知条件，利用平面向量的坐标运算的相关知识可以得到问题的答案，需要掌握坐标运算：设，则;;设，则．