题目内容
已知｛an｝是正数组成的数列，a1=1，且点（
）（n
N*）在函数y=x2+1的图象上．
（Ⅰ）求数列｛an｝的通项公式；
（Ⅱ）若数列｛bn｝满足b1=1，bn+1=bn+
，求证：bn?bn+2＜b2n+1．
解法一：
（Ⅰ）由已知得an+1=an+1、即an+1-an=1，又a1=1,
所以数列｛an｝是以1为首项，公差为1的等差数列．
故an=1+（n-1）×1=n．
（Ⅱ）由（Ⅰ）知：an=n从而bn+1-bn=2n．
bn=（bn-bn-1）+（bn-1-bn-2）+???+（b2-b1）+b1
=2n-1+2n-2+???+2+1
＝
=2n-1．
因为bn?bn+2-b
=（2n-1）（2n+2-1）-（2n+1-1）2
=（22n+2-2n+2-2n+1）-（22n+2-2?2n+1+1）
=-5?2n+4?2n
=-2n＜0,
所以bn?bn+2＜b,
解法二：
（Ⅰ）同解法一．
（Ⅱ）因为b1=1,
bn?bn+2- b=（bn+1-2n）（bn+1+2n+1）- b
=2n+1?bn+1-2n?bn+1-2n?2n+1
＝2n（bn+1-2n+1）
=2n（bn+2n-2n+1）
=2n（bn-2n）
=…
=2n（b1-2）
=-2n<0，
所以bn?bn+2<b2n+1
练习册系列答案
相关题目
+
+…+
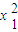，B=x1x2+x2x3+…+xn-1xn+xnx1其中x1，x2，…xn都是正数，则A≤B；
+
+
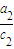的最小值为3；
+
+…+
+
的最小值为
．