题目内容
设函数f(x)=a·b,其中向量a=(m,cos2x),b=(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点 .
.
(1)求实数m的值;
(2)求函数f(x)的最小值及此时x值的集合.
解:(1)f(x)=a·b=m(1+sin2x)+cos2x,
由已知f =m
=m +cos
+cos =2,得m=1.
=2,得m=1.
(2)由(1)得f(x)=1+sin2x+cos2x =1+ sin
sin ,
,
∴当sin =-1时,f(x)取得最小值1-
=-1时,f(x)取得最小值1- ,
,
由sin =-1得,2x+
=-1得,2x+ =2kπ-
=2kπ- ,
,
即x=kπ- (k∈Z) 所以f(x)取得最小值时,x值的集合为{x|x=kπ-
(k∈Z) 所以f(x)取得最小值时,x值的集合为{x|x=kπ- ,k∈Z}
,k∈Z}

练习册系列答案
相关题目
 ,
, ,…,
,…, 来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为 分析
来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为 分析 的概率分布如下:则
的概率分布如下:则 的值为 .
的值为 .


 ,则
,则 = .
= . 是实数,
是实数, 是纯虚数,则
是纯虚数,则 D.-
D.- 的共轭复数是___________.
的共轭复数是___________.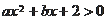 的解集为
的解集为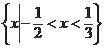 则
则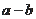 的值是 ( )
的值是 ( )