题目内容
已知双曲线![]() 设过点
设过点![]() 的直线
的直线![]() 的方向向量
的方向向量![]() .
.
(1)当直线![]() 与双曲线C的一条渐近线m平行时,求直线
与双曲线C的一条渐近线m平行时,求直线![]() 的方程及
的方程及![]() 与m 距离;
与m 距离;
(2)证明:当![]() 时,在双曲线C的右支上不存在点Q,使之到直线
时,在双曲线C的右支上不存在点Q,使之到直线![]() 的距离为
的距离为![]()
(1)![]() ,
,![]()
(2)证明见解析。
解析:
(1)双曲线C的渐近线![]()
![]() 的方程
的方程![]()
![]() 与m的距离
与m的距离![]() …………5分
…………5分
(2)证法一:设过原点且平行于![]() 的直线
的直线![]()
则直线![]() 与b的距离
与b的距离 ,
,
当![]()
又双曲线C的渐近为 ![]()
![]() 双曲线C右支在直线D的右下方
双曲线C右支在直线D的右下方
∴双曲线右支上的任意点到![]() 的距离大于
的距离大于![]()
故在双曲线C的右支上不存在点Q,使之到直线![]() 的距离为
的距离为![]() …………14分
…………14分
证法二:假设双曲线C右支上存在点![]() 到直线
到直线![]() 的距离为
的距离为![]()
则
由(1)得![]() 11分
11分
设![]()
当![]() 时,
时, ![]()
![]()
将![]() 代入(2)得
代入(2)得 ![]() (*)
(*)
![]() ,
, ![]()
![]() 方程(*)不存在正根,即假设不成立,
方程(*)不存在正根,即假设不成立,
故在双曲线C的右支上不存在点Q,使之到直线![]() 的距离为
的距离为![]() …………14分
…………14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 设过点
设过点 的直线
的直线 的方向向量
的方向向量 .
. 时,在双曲线C的右支上不存在点Q,使之到直线
时,在双曲线C的右支上不存在点Q,使之到直线
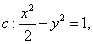 设过点
设过点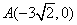 的直线l的方向向量
的直线l的方向向量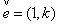
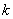 >
>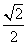 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为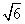 。
。