题目内容
设x=1和x=2是函数![]() 的两个极值点.
的两个极值点.
(Ⅰ)求a和b的值;
(Ⅱ)求f(x)的单调区间.
解:(Ⅰ)f′(x)=5x4+3ax2+b,
由假设知f′(1)=5+3a+ b=0,
f′(2)=24![]() 5+22
5+22![]() 3a+b=0.
3a+b=0.
解得![]()
(Ⅱ)由(Ⅰ)知
![]()
当![]() 时,f′(x)>0,
时,f′(x)>0,
当![]() 时,f′(x)<0.
时,f′(x)<0.
因此f(x)的单调增区间是![]()
f(x)的单调减区间是(-2,-1),(1,2).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+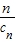 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论; ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.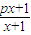 ,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an; (cn+
(cn+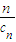 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;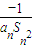 ,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.