题目内容
16.设复数z=$\frac{2}{1+i}$+(1+i)2,则复数z的共轭复数的模为( )| A. | $\sqrt{2}$ | B. | 1 | C. | 2 | D. | $\sqrt{3}$ |
分析 化简复数wa+bi的形式,求出共轭复数,然后求解即可.
解答 解:z=$\frac{2}{1+i}$+(1+i)2=$\frac{2(1-i)}{(1+i)(1-i)}$+2i=1-i+2i=1+i,
$\overline{z}$=1-i,
$\left|\overline{z}\right|=\sqrt{2}$.
故选:A.
点评 本题考查复数的基本运算,复数的模的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若复数$\frac{1+bi}{2+i}$是纯虚数(i是虚数单位,b是实数),则b=( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
6.设集合A={x|(x+1)(x-2)<0},集合B={x|1<x<3},则A∪B=( )
| A. | {x|-1<x<3} | B. | {x|-1<x<1} | C. | {x|1<x<2} | D. | {x|2<x<3} |
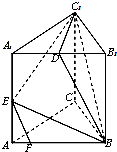 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB. 如图,已知PE为圆eO的切线,切点为E,割线PBA交eO于A、B两点,C为AE上一点,且∠CPE=∠CPA.
如图,已知PE为圆eO的切线,切点为E,割线PBA交eO于A、B两点,C为AE上一点,且∠CPE=∠CPA.