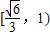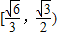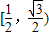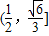题目内容
已知正△ABC的顶点A在平面α内,顶点B,C在平面α的同一侧,D为BC的中点,若△ABC在平面α内的射影是以A为直角顶点的三角形,则直线AD与平面α所成角的正弦值的最小值为 .
【答案】分析:而当BC∥α时,其B、D、C三点的射影分别为B1,D1,C1时,且∠B1AC1=90°.∠DAD1为直线AD与平面α所成角且最小.求出即可.
解答:解:如图所示, 不妨设AB=2.则AD=
不妨设AB=2.则AD= .
.
假设一开始正△ABC在平面α内时的位置,则∠BAC=60°.
而当BC∥α时,其B、D、C三点的射影分别为B1,D1,C1时,且∠B1AC1=90°.
∠DAD1为直线AD与平面α所成角且最小.
则 ,∴
,∴ =
= .
.
此时 =
= .
.
当BC与平面α部平行时,可以看出:其DD1长度必然增大.
因此直线AD与平面α所成角的正弦值的最小值为 .
.
故答案为 .
.
点评:正确找出直线AD与平面α所成角的正弦值的最小值时的位置是解题的关键.
解答:解:如图所示,
 不妨设AB=2.则AD=
不妨设AB=2.则AD= .
.假设一开始正△ABC在平面α内时的位置,则∠BAC=60°.
而当BC∥α时,其B、D、C三点的射影分别为B1,D1,C1时,且∠B1AC1=90°.
∠DAD1为直线AD与平面α所成角且最小.
则
 ,∴
,∴ =
= .
.此时
 =
= .
.当BC与平面α部平行时,可以看出:其DD1长度必然增大.
因此直线AD与平面α所成角的正弦值的最小值为
 .
.故答案为
 .
.点评:正确找出直线AD与平面α所成角的正弦值的最小值时的位置是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
已知正△ABC的顶点A在平面α上,顶点B,C在平面α的同一侧,D为BC的中点,若△ABC在平面α上的射影是以A为直角顶点的三角形,则直线AD与平面α所成角的正弦值的范围是( )
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、(
|