题目内容
某工厂生产甲、乙两种产品,每生产一吨产品所消耗的电能和煤、所需工人人数以及所得产值如下表所示:品种 | 电能(千度) | 煤(吨) | 工人人数(人) | 产值(万元) |
甲 | 2 | 3 | 5 | 7 |
乙 | 8 | 5 | 2 | 10 |
已知该工厂的工人人数最多是200人,根据限额,该工厂每天消耗电能不得超过160千度,消耗煤不得超过150吨,问怎样安排甲、乙两种产品的生产数量,才能使每天所得的产值最大?
解:设甲、乙两种产品每天分别生产x吨和y吨,则每天所得的产值为z=7x+10y万元.
依题意,得不等式组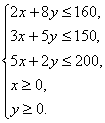 (*)
(*)
由![]() 解得
解得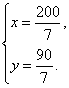
由![]() 解得
解得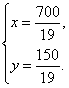
设点A的坐标为(![]() ,
,![]() ),点B的坐标为(
),点B的坐标为(![]() ,
,![]() ),则不等式组(*)所表示的平面区域是四边形的边界及其内部(如图中阴影部分).
),则不等式组(*)所表示的平面区域是四边形的边界及其内部(如图中阴影部分).
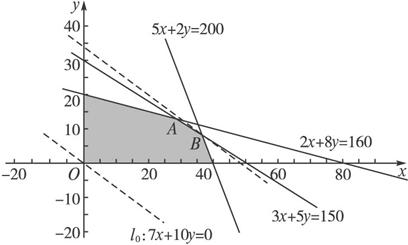
令z=0,得7x+10y=0,即y=![]() x.
x.
作直线l0:y=![]() x.
x.
由图可知把l0平移至过点B(![]() ,
,![]() ),即x=
),即x=![]() ,y=
,y=![]() 时,z取得最大值
时,z取得最大值![]() .
.
答:每天生产甲产品![]() 吨、乙产品
吨、乙产品![]() 吨时,能获得最大的产值为
吨时,能获得最大的产值为![]() 万元.
万元.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 18、某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级,对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品
18、某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有A、B两个等级,对每种产品,两道工序的加工结果都为A级时,产品为一等品,其余均为二等品