题目内容
设函数f(x)=a|x|+ (a,b为常数),且①f(-2)=0;②f(x)有两个单调递增区间,则同时满足上述条件的一个有序数对(a,b)为________.
(a,b为常数),且①f(-2)=0;②f(x)有两个单调递增区间,则同时满足上述条件的一个有序数对(a,b)为________.
满足(t,4t)(t<0)的任一组解均可
分析:由f(-2)=2a-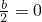 可得b=4a,从而可得
可得b=4a,从而可得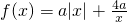 =
=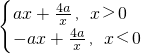 ,由函数的定义域为(-∞,0)(0,+∞),当a>0时,函数在(2,+∞)单调递增,在(-∞,0),(0,2)单调递减,当a<0时,函数在(0,+∞)在(0,2)单调递增,在(-∞,0)单调递减,当a=0时,函数f(x)=0不具有单调性,从而可得
,由函数的定义域为(-∞,0)(0,+∞),当a>0时,函数在(2,+∞)单调递增,在(-∞,0),(0,2)单调递减,当a<0时,函数在(0,+∞)在(0,2)单调递增,在(-∞,0)单调递减,当a=0时,函数f(x)=0不具有单调性,从而可得
解答:由f(-2)=2a-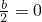 可得,b=4a
可得,b=4a
∴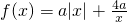 =
=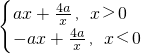
∴函数的定义域为(-∞,0)(0,+∞)
∵f(x)有两个单调递增区间
当a>0时,函数在(2,+∞)单调递增,在(-∞,0),(0,2)单调递减,不符合题意
当a<0时,函数在(0,+∞)在(0,2)单调递增,在(-∞,0)单调递减
当a=0时,函数f(x)=0不具有单调性
故满足条件的a<0
故答案为:(t,4t)(t<0)
点评:本题主要考查了形如f(x)=ax+ 的单调性与参数a的取值范围的关系,解题的关键是要灵活利用基本初等函数的单调行.
的单调性与参数a的取值范围的关系,解题的关键是要灵活利用基本初等函数的单调行.
分析:由f(-2)=2a-
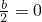 可得b=4a,从而可得
可得b=4a,从而可得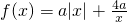 =
=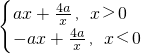 ,由函数的定义域为(-∞,0)(0,+∞),当a>0时,函数在(2,+∞)单调递增,在(-∞,0),(0,2)单调递减,当a<0时,函数在(0,+∞)在(0,2)单调递增,在(-∞,0)单调递减,当a=0时,函数f(x)=0不具有单调性,从而可得
,由函数的定义域为(-∞,0)(0,+∞),当a>0时,函数在(2,+∞)单调递增,在(-∞,0),(0,2)单调递减,当a<0时,函数在(0,+∞)在(0,2)单调递增,在(-∞,0)单调递减,当a=0时,函数f(x)=0不具有单调性,从而可得解答:由f(-2)=2a-
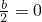 可得,b=4a
可得,b=4a∴
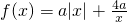 =
=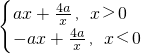
∴函数的定义域为(-∞,0)(0,+∞)
∵f(x)有两个单调递增区间
当a>0时,函数在(2,+∞)单调递增,在(-∞,0),(0,2)单调递减,不符合题意
当a<0时,函数在(0,+∞)在(0,2)单调递增,在(-∞,0)单调递减
当a=0时,函数f(x)=0不具有单调性
故满足条件的a<0
故答案为:(t,4t)(t<0)
点评:本题主要考查了形如f(x)=ax+
 的单调性与参数a的取值范围的关系,解题的关键是要灵活利用基本初等函数的单调行.
的单调性与参数a的取值范围的关系,解题的关键是要灵活利用基本初等函数的单调行. 
练习册系列答案
相关题目
设函数f(x)=a+bcosx+csinx的图象过点(0,1)和点(
,1),当x∈[0,
]时,|f(x)|<2,则实数a的取值范围是( )
| π |
| 2 |
| π |
| 2 |
A、-
| ||||
B、1≤a<4+3
| ||||
C、-
| ||||
| D、-a<a<2 |