题目内容
已知函数f(x)=2sinxcosx+2cos2x(x∈R).
(Ⅰ)求f(x)的最小正周期,并求f(x)的最小值;
(Ⅱ)令 ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由.
解:(Ⅰ) ,
,
其最小正周期是 ,
,
又当 ,
,
即 时,
时,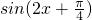 取得最小值-1,
取得最小值-1,
所以函数f(x)的最小值是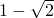 ,此时x的集合为
,此时x的集合为 . (7分)
. (7分)
(Ⅱ)
∵ .
.
∴函数g(x)是偶函数. (7分)
分析:(I)根据二倍角公式,和辅助角公式,我们易将函数f(x)=2sinxcosx+2cos2x化成正弦型函数,进而根据正弦型函数的性质判断出f(x)的最小正周期,并求f(x)的最小值.
(II)根据函数图象的平移变换法则,我们易求出函数g(x)的解析式,根据余弦型函数的性质,我们易得到函数g(x)的奇偶性,根据奇偶性的定义,易给出证明.
点评:本题考查的知识点是三角函数中恒等变换应用,三角函数的周期性及其求法,三角函数的最值,熟练掌握正弦型函数和余弦型函数的性质是解答本题的关键.
 ,
,其最小正周期是
 ,
,又当
 ,
,即
 时,
时,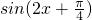 取得最小值-1,
取得最小值-1,所以函数f(x)的最小值是
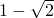 ,此时x的集合为
,此时x的集合为 . (7分)
. (7分)(Ⅱ)

∵
 .
.∴函数g(x)是偶函数. (7分)
分析:(I)根据二倍角公式,和辅助角公式,我们易将函数f(x)=2sinxcosx+2cos2x化成正弦型函数,进而根据正弦型函数的性质判断出f(x)的最小正周期,并求f(x)的最小值.
(II)根据函数图象的平移变换法则,我们易求出函数g(x)的解析式,根据余弦型函数的性质,我们易得到函数g(x)的奇偶性,根据奇偶性的定义,易给出证明.
点评:本题考查的知识点是三角函数中恒等变换应用,三角函数的周期性及其求法,三角函数的最值,熟练掌握正弦型函数和余弦型函数的性质是解答本题的关键.

练习册系列答案
相关题目