题目内容

若动圆P过点N（-2，0），且与另一圆M：（x-2）2+y2=8相外切，则动圆P的圆心的轨迹方程是
x2
2
-
y2
2
=1（x＜0）
x2
2
-
y2
2
=1（x＜0）
．
分析：根据题意可推断出|PM|-|PN|=2
2
＜|MN|=4进而利用双曲线的定义可知点P的轨迹W是以M、N为焦点的双曲线的右支，依题意求得a和c，则b可求，进而求得双曲线的方程．
解答：解：设动圆半径为r，则|PN|=r，|PM|=r+2
2
，
因此|PM|-|PN|=2
2
，
这说明动圆的圆心P到M的距离与到N的距离之差为定值2
2
，
因此由定义知，P的轨迹是以M、N为焦点的双曲线的左支．
因为2a=2
2
，所以a=
2
，
∵c=2，∴b2=c2-a2=2
∴所求轨迹方程为
x2
2
-
y2
2
=1（x＜0）
故答案为
x2
2
-
y2
2
=1（x＜0）
点评：本题考查轨迹方程，考查双曲线的定义，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
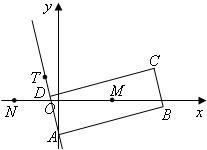精英家教网如图，矩形ABCD的两条对角线相交于点M（2，0），AB边所在直线的方程为x-3y-6=0点T（-1，1）在AD边所在直线上．
（Ⅰ）求AD边所在直线的方程；
（Ⅱ）求矩形ABCD外接圆的方程；
（Ⅲ）若动圆P过点N（-2，0），且与矩形ABCD的外接圆外切，求动圆P的圆心的轨迹方程．
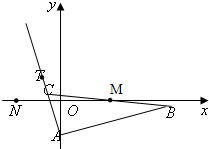精英家教网已知△ABC的边AB边所在直线的方程为x-3y-6=0，M（2，0）满足
BM
=
MC
，点T（-1，1）在AC边所在直线上且满足
AT
=
AB
．
（I）求AC边所在直线的方程；
（II）求△ABC外接圆的方程；
（III）若动圆P过点N（-2，0），且与△ABC的外接圆外切，求动圆P的圆心的轨迹方程．
请注意下面两题用到求和符号：
f（k）+f（k+1）+f（k+2）+…+f（n）=
n
i=k
f(i)，其中k，n为正整数且k≤n．
（2012•东莞二模）已知△ABC的边AB边所在直线的方程为x-3y-6=0，M（2，0）满足
BM
=
MC
，点T（-1，1）在AC边所在直线上且满足
AT
•
AB
=0．
（1）求AC边所在直线的方程；
（2）求△ABC外接圆的方程；
（3）若动圆P过点N（-2，0），且与△ABC的外接圆外切，求动圆P的圆心的轨迹方程．
已知△ABC的边AB边所在直线的方程为x-3y-6=0，M（2，0）满足，点T（-1，1）在AC边所在直线上且满足．
（1）求AC边所在直线的方程；
（2）求△ABC外接圆的方程；
（3）若动圆P过点N（-2，0），且与△ABC的外接圆外切，求动圆P的圆心的轨迹方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网