题目内容
设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2.若对任意的x∈[a,a+2],不等式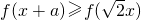 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是
- A.a≤0
- B.
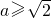
- C.
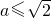
- D.a≥0
B
分析:由题意可知f(x)为R上的增函数,故对任意的x∈[a,a+2],不等式f(x+a)≥2f(x)恒成立可转化为x+a≥ x对任意的x∈[a,a+2]恒成立,此为一次不等式恒成立,解决即可.利用特值法相对简单.
x对任意的x∈[a,a+2]恒成立,此为一次不等式恒成立,解决即可.利用特值法相对简单.
解答:(排除法)当a=0时,则x∈[0,2],
由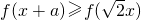 得f(x)≥f(
得f(x)≥f( x),即x2≥2x2?x2≤0在x∈[0,2]时恒成立,显然不成立,排除A、C、D,
x),即x2≥2x2?x2≤0在x∈[0,2]时恒成立,显然不成立,排除A、C、D,
故选B.
点评:本题考查函数单调性的应用:利用单调性处理不等式恒成立问题.将不等式化为f(a)≥f(b)形式是解题的关键,本题采用了特值法,使运算过程大大减少,注意体会.
分析:由题意可知f(x)为R上的增函数,故对任意的x∈[a,a+2],不等式f(x+a)≥2f(x)恒成立可转化为x+a≥
 x对任意的x∈[a,a+2]恒成立,此为一次不等式恒成立,解决即可.利用特值法相对简单.
x对任意的x∈[a,a+2]恒成立,此为一次不等式恒成立,解决即可.利用特值法相对简单.解答:(排除法)当a=0时,则x∈[0,2],
由
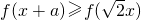 得f(x)≥f(
得f(x)≥f( x),即x2≥2x2?x2≤0在x∈[0,2]时恒成立,显然不成立,排除A、C、D,
x),即x2≥2x2?x2≤0在x∈[0,2]时恒成立,显然不成立,排除A、C、D,故选B.
点评:本题考查函数单调性的应用:利用单调性处理不等式恒成立问题.将不等式化为f(a)≥f(b)形式是解题的关键,本题采用了特值法,使运算过程大大减少,注意体会.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |