Question

已知数列{a_n}的前n项和为S_n,其满足a₁=1,3S_n=(n+2)a_n,问是否存在实数a、b、c使得a_n=a·n²+b·n+c对一切n∈N*都成立?若存在,求出a,b,c;若不存在,请说明理由.

Answer 1

分析：本题是一道探索性问题,可从假设结论成立入手.

解：假设满足条件的a,b,c存在,将n=2,3代入3S_n=(n+2)a_n中,可得a₂=3,a₃=6.

代入a_n=an²+bn+c中,可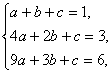得     解得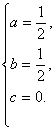

∴a_n=n²+n.      

证明:(1)当n=1时,命题成立.

(2)假设当n=k(k∈N*)时命题成立,即a_k=k²+k,

那么由a_k+1=S_k+1-S_k=a_k+1-a_k,                       

得a_k+1=a_k=(k²+k)=(k+2)(k+1)=(k+1)²+(k+1).

也就是说,当n=k+1时等式也成立.

根据(1)、(2)可知,对任何n∈N*等式都成立.