题目内容
6.观察下列等式:n•C${\;}_{n-1}^{0}$=1$•{C}_{n}^{1}$,
n$•{C}_{n-1}^{1}$=2$•{C}_{n}^{2}$,
n$•{C}_{n-1}^{2}$=3$•{C}_{n}^{3}$,
n$•{C}_{n-1}^{3}$=4$•{C}_{n}^{4}$,
n$•{C}_{n-1}^{4}$=5$•{C}_{n}^{5}$,
…
则归纳出一般的结论为n$•{C}_{n-1}^{k}$=(k+1)$•{C}_{n-1}^{k+1}$.
分析 由已知中n•C${\;}_{n-1}^{0}$=1$•{C}_{n}^{1}$,n$•{C}_{n-1}^{1}$=2$•{C}_{n}^{2}$,n$•{C}_{n-1}^{2}$=3$•{C}_{n}^{3}$,n$•{C}_{n-1}^{3}$=4$•{C}_{n}^{4}$,n$•{C}_{n-1}^{4}$=5$•{C}_{n}^{5}$,…归纳出等式两边数的变化规律,可得答案.
解答 解:由已知中:
n•C${\;}_{n-1}^{0}$=1$•{C}_{n}^{1}$,
n$•{C}_{n-1}^{1}$=2$•{C}_{n}^{2}$,
n$•{C}_{n-1}^{2}$=3$•{C}_{n}^{3}$,
n$•{C}_{n-1}^{3}$=4$•{C}_{n}^{4}$,
n$•{C}_{n-1}^{4}$=5$•{C}_{n}^{5}$,
…
归纳可得:n$•{C}_{n-1}^{k}$=(k+1)$•{C}_{n-1}^{k+1}$,
故答案为:n$•{C}_{n-1}^{k}$=(k+1)$•{C}_{n-1}^{k+1}$
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知某简谐运动的图象经过点(0,2),且对应函数的解析式为f(x)=4sin($\frac{π}{3}$x+φ)(|φ|<$\frac{π}{2}$),则该简谐运动的初相φ的值为( )
| A. | φ=$\frac{π}{3}$ | B. | φ=$\frac{π}{4}$ | C. | φ=$\frac{π}{5}$ | D. | φ=$\frac{π}{6}$ |
16.某项测试要过两关,第一关有3种测试方案,第二关有5种测试方案,某人参加该项测试,不同的测试方法种数为( )
| A. | 3+5 | B. | 3×5 | C. | 35 | D. | 53 |
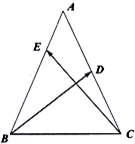 如图,在△ABC中,已知AB=AC=$\sqrt{6}$,AD=DC,$\overrightarrow{AB}$=3$\overrightarrow{AE}$,若$\overrightarrow{BD}•\overrightarrow{AC}$=-$\frac{1}{2}$,则$\overrightarrow{BD}•\overrightarrow{CE}$等于$-\frac{11}{12}$.
如图,在△ABC中,已知AB=AC=$\sqrt{6}$,AD=DC,$\overrightarrow{AB}$=3$\overrightarrow{AE}$,若$\overrightarrow{BD}•\overrightarrow{AC}$=-$\frac{1}{2}$,则$\overrightarrow{BD}•\overrightarrow{CE}$等于$-\frac{11}{12}$.