题目内容
已知椭圆的中心在坐标原点,离心率为 ,一个焦点是F(0,1).
,一个焦点是F(0,1).
(Ⅰ)求椭圆方程;
(Ⅱ)直线l过点F交椭圆于A、B两点,且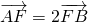 ,求直线l的方程.
,求直线l的方程.
解:(Ⅰ)设椭圆方程为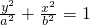 (a>b>0).
(a>b>0).
依题意,e= =
= ,c=1,∴a=2,b2=a2-c2=3,
,c=1,∴a=2,b2=a2-c2=3,
∴所求椭圆方程为 ;
;
(Ⅱ)若直线l的斜率k不存在,则不满足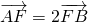 .
.
当直线l的斜率k存在时,设直线l的方程为y=kx+1.
因为直线l过椭圆的焦点F(0,1),所以k取任何实数,直线l与椭圆均有两个交点A、B.
设A(x1,y1),B(x2,y2),
联立方程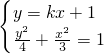 消去y,得(3k2+4)x2+6kx-9=0.
消去y,得(3k2+4)x2+6kx-9=0.
∴x1+x2=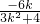 ,①x1•x2=
,①x1•x2=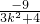 ,②
,②
由F(0,1),A(x1,y1),B(x2,y2),
则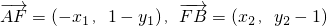 ,
,
∵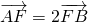 ,∴(-x1,1-y1)=2(x2,y2-1),得x1=-2x2.
,∴(-x1,1-y1)=2(x2,y2-1),得x1=-2x2.
将x1=-2x2代入①、②,得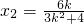 ,③
,③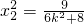 ,④
,④
由③、④得,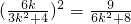 ,化简得
,化简得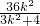 =
= ,
,
解得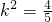 ,∴k=±
,∴k=±
∴直线l的方程为:y=± x+1.
x+1.
分析:(Ⅰ)设椭圆方程,确定几何量,即可得到椭圆方程;
(Ⅱ)分类讨论,设出直线方程与椭圆方程联立,利用韦达定理及向量条件,即可求得直线方程.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识,考查学生分析解决问题的能力,属于中档题.
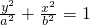 (a>b>0).
(a>b>0).依题意,e=
 =
= ,c=1,∴a=2,b2=a2-c2=3,
,c=1,∴a=2,b2=a2-c2=3,∴所求椭圆方程为
 ;
;(Ⅱ)若直线l的斜率k不存在,则不满足
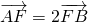 .
.当直线l的斜率k存在时,设直线l的方程为y=kx+1.
因为直线l过椭圆的焦点F(0,1),所以k取任何实数,直线l与椭圆均有两个交点A、B.
设A(x1,y1),B(x2,y2),
联立方程
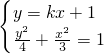 消去y,得(3k2+4)x2+6kx-9=0.
消去y,得(3k2+4)x2+6kx-9=0.∴x1+x2=
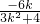 ,①x1•x2=
,①x1•x2=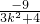 ,②
,②由F(0,1),A(x1,y1),B(x2,y2),
则
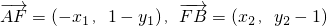 ,
,∵
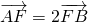 ,∴(-x1,1-y1)=2(x2,y2-1),得x1=-2x2.
,∴(-x1,1-y1)=2(x2,y2-1),得x1=-2x2.将x1=-2x2代入①、②,得
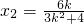 ,③
,③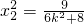 ,④
,④由③、④得,
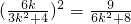 ,化简得
,化简得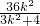 =
= ,
,解得
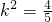 ,∴k=±
,∴k=±
∴直线l的方程为:y=±
 x+1.
x+1.分析:(Ⅰ)设椭圆方程,确定几何量,即可得到椭圆方程;
(Ⅱ)分类讨论,设出直线方程与椭圆方程联立,利用韦达定理及向量条件,即可求得直线方程.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.
已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.