题目内容
如图,在正方体AC'中,E是A'D的中点,F是正方形ABCD的中心,求
与
的夹角.
| D′E |
| FC′ |


以DA所在直线为x轴,DB所在直线为y轴,DD′所在直线为z轴,建立空间直角坐标系.
设正方形边长为2,
则D点为原点,D′(0,0,2),E(1,0,1),F(1,1,0),C′(0,2,2)
∴
| D′E |
| FC′ |
∴cos<
| D′E |
| FC′ |
| ||||
|
|
| -1+0-2 | ||||
|
| -3 | ||
2
|
| ||
| 2 |
∵向量夹角的范围为[0,π]
∴
| D′E |
| FC′ |

练习册系列答案
相关题目
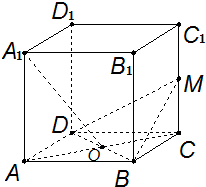 如图,在正方体ABCD-A1B1C1D1中,M为CC1的中点,AC交BD于点O,求证:A1O⊥平面MBD.
如图,在正方体ABCD-A1B1C1D1中,M为CC1的中点,AC交BD于点O,求证:A1O⊥平面MBD.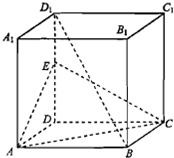 如图:在正方体ABCD-A1B1C1D1中,E为棱DD1的中点
如图:在正方体ABCD-A1B1C1D1中,E为棱DD1的中点 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点,
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点, 如图,在正方体AC'中,E是A'D的中点,F是正方形ABCD的中心,求
如图,在正方体AC'中,E是A'D的中点,F是正方形ABCD的中心,求