题目内容
如图，在梯形
中，
，
，
，
、
分别是
、
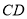上的点，
，
，沿将梯形翻折，使平面
平面
，
是
的中点.
（1）当
时，求证：
；
（2）当
变化时，求三棱锥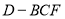
的体积的最大值.
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
培优三好生系列答案优化作业上海科技文献出版社系列答案题目内容
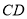如图，在梯形中，，，，、分别是、上的点，，，沿将梯形翻折，使平面平面，是的中点.
（1）当时，求证：；
（2）当变化时，求三棱锥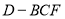的体积的最大值.
培优三好生系列答案优化作业上海科技文献出版社系列答案
，
．
时，求函数
的单调区间及所有零点；
，
，
为函数
图象上的三个不同点，且
，问：是否存在实数
，使得函数
在点
处的切线与直线
平行？若存在，求出所有满足条件的实数
的值；若不存在，请说明理由．
对应的点位于（ ）
的焦点
作直线
与其交于
两点，若
，则
（ ）
D．1
为纯虚数，则
（ ）
、
、
、
四位同学周五下午参加学校的课外活动，在课外活动时间中，有一人在打篮球，有一人在画画，有一人在跳舞，另外一人在散步.
不在散步，也不在打篮球；
不在跳舞，也不在跑步；
在散步”是“
在跳舞”的充分条件；
不在打篮球，也不在跑步；
不在跳舞，也不在打篮球.
在 .
上的函数
满足
，
，且
时，
，则
（ ）
B.
，则
展开式中的常数项为 （用数字做答）
中，
平面
，
平面
，
.
平面
；
为线段
（含端点）上一点，设直线
与平面
所成角为
，求
的取值范围.