题目内容
如图，在底面为直角梯形的四棱锥P-ABCD中AD∥BC，PD⊥平面ABCD，AD=1，AB=| 3 |
（Ⅰ）求证：BD⊥PC；
（Ⅱ）求直线AB与平面PDC所成的角；
（Ⅲ）设点E在棱PC上，
| PE |
| PC |
分析：如图，在平面ABCD内过D作直线DF∥AB，交BC于F，分别以DA、DF、DP所在的直线为x、y、z轴建立空间直角坐标系．
（1）只要证明
•
=0，即可得到BD⊥PC；
（2）由（1）即可得到平面PDC的法向量为
，求出
，求出向量
与
的夹角，即可得到线面角；
（3）先求出平面PAB的法向量
，若DE∥平面PAB，则
•
=0，即可得出λ．
（1）只要证明
| BD |
| PC |
（2）由（1）即可得到平面PDC的法向量为
| DB |
| AB |
| DB |
| AB |
（3）先求出平面PAB的法向量
| n |
| n |
| DE |
解答：解：如图，在平面ABCD内过D作直线DF∥AB，交BC于F，分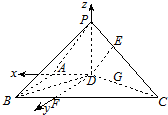
别以DA、DF、DP所在的直线为x、y、z轴建立空间直角坐标系．
（1）证明：设PD=a，得B(1，
，0)，P（0，0，a），C(-3，
，0)，
则
=(-1，-
，0)，
=(-3，
，-a)，
∵
•
=3-3=0，
∴BD⊥PC．
（2）由（1）知BD⊥面PDC，
就是平面PDC的法向量．
由条件知A（1，0，0），B（1，
，0），
=(0，
，0) ，
=(1，
，0)．
设AB与面PDC所成角大小为θ，
则sinθ=
=
=
．
∵0°＜θ＜90°，∴θ=60°，
即直线AB与平面PDC所成角为60°．
（3）由（2）知C（-3，
，0），记P（0，0，a），
则
=(0 ，
， 0)，
=(0 ， 0 ， a)，
=(1，0，-a)，
=(-3 ，
，-a)，
而
=λ
，∴
=(-3λ ，
λ ，aλ)，
=
+
=
+λ
=(0，0，a)+(-3λ ，
λ ，-aλ)=(-3λ ，
λ ，a-aλ)．
设
=(x，y，z)为平面PAB的法向量，则
，即
，即
．
取z=1，得x=a，进而得
=(a ， 0 ， 1)，
由DE∥平面PAB，得
•
=0，∴-3aλ+a-aλ=0，而a≠0，∴λ=
．
别以DA、DF、DP所在的直线为x、y、z轴建立空间直角坐标系．
（1）证明：设PD=a，得B(1，
| 3 |
| 3 |
则
| BD |
| 3 |
| PC |
| 3 |
∵
| BD |
| PC |
∴BD⊥PC．
（2）由（1）知BD⊥面PDC，
| DB |
由条件知A（1，0，0），B（1，
| 3 |
| AB |
| 3 |
| DB |
| 3 |
设AB与面PDC所成角大小为θ，
则sinθ=
| ||||
|
|
| 3 | ||
2
|
| ||
| 2 |
∵0°＜θ＜90°，∴θ=60°，
即直线AB与平面PDC所成角为60°．
（3）由（2）知C（-3，
| 3 |
则
| AB |
| 3 |
| DP |
| PA |
| PC |
| 3 |
而
| PE |
| PC |
| PE |
| 3 |
| DE |
| DP |
| PE |
| DP |
| PC |
| 3 |
| 3 |
设
| n |
|
|
|
取z=1，得x=a，进而得
| n |
由DE∥平面PAB，得
| DE |
| n |
| 1 |
| 4 |
点评：熟练掌握通过建立空间直角坐标系．利用向量垂直与数量积的关系、平面PDC的法向量为
与斜线
的夹角得到线面角、DE∥平面PAB?
•
=0等是解题的关键．
| DB |
| AB |
| n |
| DE |
练习册系列答案
相关题目
如图，已知棱锥P-ABCD的底面ABCD为直角梯 形，AB∥CD，AB⊥BC，CD=PB=BC=1，
如图，在四棱锥P-ABCD中，底面为直角梯ABCD，AD∥BC，∠BAD=90°，PA⊥底面ABCD，且PA=AD=AB=2BC，M，N分别为PC，PB的中点．
如图，在四棱锥P-ABCD中，底面为直角梯ABCD，AD∥BC，∠BAD=90°，PA⊥底面ABCD，且PA=AD=AB=2BC，M，N分别为PC，PB的中点．
