题目内容
在自然条件下,某草原上野兔第n年年初的数量记为xn,该年的增长量yn和 xn与 的乘积成正比,比例系数为
的乘积成正比,比例系数为 ,其中m是与n无关的常数,且x1<m,
,其中m是与n无关的常数,且x1<m,
(1)证明: ;
;
(2)用 xn表示xn+1;并证明草原上的野兔总数量恒小于m.
(1)由题意知 ,配方得:
,配方得: ∵
∵ ∴当且仅当
∴当且仅当 时,
时, 取得最大值
取得最大值 ,即
,即 (5分)
(5分)
(2) (8分)
(8分)
用数列归纳法证明:
当n=1时,由题意知 ,故命题成立
,故命题成立
假设当 时,命题成立
时,命题成立
 是xk的一个二次函数
是xk的一个二次函数 ,
, 有对称轴
有对称轴 ,开口向下,由
,开口向下,由 ,则
,则 ,于是在
,于是在 上均有
上均有 =m
=m
取 ,即知
,即知 ,∴当
,∴当 时,命题成立,综上知,对一切正整数n,
时,命题成立,综上知,对一切正整数n, 这就是说该草原上的野兔数量不可能无限增长
这就是说该草原上的野兔数量不可能无限增长

练习册系列答案
相关题目
 中,直线
中,直线 过点
过点 且倾斜角为
且倾斜角为 ,在极坐标系(与直角坐标系
,在极坐标系(与直角坐标系 为极点,
为极点, 轴的正半轴为极轴)中,圆
轴的正半轴为极轴)中,圆 的方程为
的方程为 。
。 两点,若点
两点,若点 的坐标为
的坐标为 。
。 在点
在点 处的切线方程为
处的切线方程为 ,类似地,可以求得椭圆
,类似地,可以求得椭圆 在
在 处的切线方程为________.
处的切线方程为________.
 的最小正周期
的最小正周期 时,若
时,若 ,求
,求 的值
的值 B、
B、 C、18
C、18 D、20
D、20

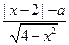 为奇函数,则f(
为奇函数,则f(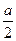 )= 。
)= 。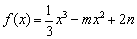 (
(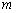 ,
,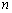 为常数),当
为常数),当 时,函数
时,函数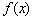 有极值,若函数
有极值,若函数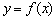 有且只有三个零点,则实数
有且只有三个零点,则实数