题目内容
已知函数f(x)=
，下列命题正确的是
①f（x）是奇函数
②对定义域内任意x，f（x）＜1恒成立；
③当x=
π时，f（x）取得极小值；
④f（2）＞f（3）
⑤当x＞0时，若方程|f（x）|=k有且仅有两个不同的实数解α，β（α＞β）则β•cosα=-α•sinβ
| sinx |
| x |
②④
②④
．（写出所有正确命题的序号）①f（x）是奇函数
②对定义域内任意x，f（x）＜1恒成立；
③当x=
| 3 |
| 2 |
④f（2）＞f（3）
⑤当x＞0时，若方程|f（x）|=k有且仅有两个不同的实数解α，β（α＞β）则β•cosα=-α•sinβ
分析：判断出函数的奇偶性，可判断①，求出函数的值域，可判断②；判断出函数的极值点，可判断③；利用函数的单调性，比较两个函数值，可判断④，数形结合分析出βcosα=-sinβ，可判断⑤．
解答：解：①函数的定义域是{x|x≠0，x∈R}，f（-x）=
=
=f（x），∴f（x）是偶函数，故①错误；
②∵根据三角函数线的定义知|sinx|≤|x|，∴
≤1，∵x≠0，∴
＜1成立，故②正确；
③∵f′（x）=
，∵f′（
）=
≠0，∴x=
不是极值点，∴③错误；
④∵
＜2＜3＜π，∴sin2＞sin3＞0，∴
＞
，∴④正确；
⑤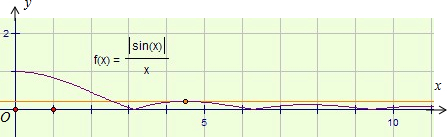
因为|
|=k（ x＞0）有且仅有两个不同的根α，β，所以，k＞0
因为x＞0时，y=sinx为周期函数，y=x为增函数
所以，f（x）在（0，π）的最大值＞f（x）在（π，2π）的最大值＞f（x）在（2π，3π）的最大值＞…
因为，α＞β
所以，α必为y=f（x）在（π，2π）取最大值时x的值，
π＜x＜2π时，f（x）=|
|=-
f'（x）=
，令f'（x）=0，
则αcosα-sinα=0，即cosα=
，
所以，f（α）=-
=-cosα=k
α，β为方程f（x）=k在（0，π）的根
所以，
=k
所以，
=-cosα
即：βcosα=-sinβ，故⑤错误
故答案为：②④
| sin(-x) |
| -x |
| sinx |
| x |
②∵根据三角函数线的定义知|sinx|≤|x|，∴
| |sinx| |
| |x| |
| sinx |
| x |
③∵f′（x）=
| xcosx-sinx |
| x2 |
| 3π |
| 2 |
| 4 |
| 9π2 |
| 3π |
| 2 |
④∵
| π |
| 2 |
| sin2 |
| 2 |
| sin3 |
| 3 |
⑤
因为|
| sinx |
| x |
因为x＞0时，y=sinx为周期函数，y=x为增函数
所以，f（x）在（0，π）的最大值＞f（x）在（π，2π）的最大值＞f（x）在（2π，3π）的最大值＞…
因为，α＞β
所以，α必为y=f（x）在（π，2π）取最大值时x的值，
π＜x＜2π时，f（x）=|
| sinx |
| x |
| sinx |
| x |
f'（x）=
| -xcosx+sinx |
| x2 |
则αcosα-sinα=0，即cosα=
| sinα |
| α |
所以，f（α）=-
| sinα |
| α |
α，β为方程f（x）=k在（0，π）的根
所以，
| sinβ |
| β |
所以，
| sinβ |
| β |
即：βcosα=-sinβ，故⑤错误
故答案为：②④
点评：本题以命题的真假判断为载体考查了三角函数的奇偶性，值域，极值，单调性是三角函数图象和性质的综合应用，难度较大．
练习册系列答案
相关题目
将正奇数列{2n-1}中的所有项按每一行比上一行多一项的规则排成如下数表：