题目内容
规定 其中
其中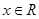 ,
,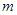 为正整数,且
为正整数,且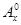 =1,这是排列数
=1,这是排列数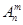 (
(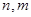 是正整数,
是正整数,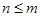 )的一种推广.
)的一种推广.
(Ⅰ) 求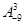 的值;
的值;
(Ⅱ)排列数的两个性质:①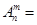
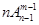 ,②
,②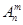
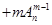
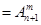 (其中m,n是正整数).是否都能推广到
(其中m,n是正整数).是否都能推广到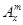 (
(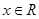 ,
,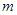 是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(Ⅲ)已知函数 ,试讨论函数
,试讨论函数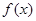 的零点个数.
的零点个数.
【答案】
(1)-990
(2)①
 ,②
,②

 (
( )
)
(3)当 时,函数
时,函数 不存在零点,
不存在零点,
当 时,函数
时,函数 有且只有一个零点,
有且只有一个零点,
当 时,即函数
时,即函数 有且只有两个零点.
有且只有两个零点.
【解析】
试题分析:解:(Ⅰ)
(Ⅱ)性质①、②均可推广,推广的形式分别是①
 ,②
,②

 (
( )
)
证明:①当 时,左边
时,左边 ,右边
,右边 ,等式成立;
,等式成立;
当 时,左边
时,左边

因此,
 (
( )成立.
)成立.
②当 时,左边
时,左边 右边,等式成立;
右边,等式成立;
当 时,左边
时,左边



 =右边
=右边
因此,

 (
( )成立.
)成立.
(Ⅲ)
设函数 ,
,
则函数 零点的个数等价于函数
零点的个数等价于函数 与
与 公共点的个数.
公共点的个数.
 的定义域为
的定义域为

令 ,得
,得
|
|
|
|
|
|
|
- |
0 |
+ |
|
|
减 |
|
增 |
∴当 时,函数
时,函数 与
与 没有公共点,即函数
没有公共点,即函数 不存在零点,
不存在零点,
当 时,函数
时,函数 与
与 有一个公共点,即函数
有一个公共点,即函数 有且只有一个零点,
有且只有一个零点,
当 时,函数
时,函数 与
与 有两个公共点,即函数
有两个公共点,即函数 有且只有两个零点.
有且只有两个零点.
考点:函数零点
点评:主要是考查了函数零点的求解以及组合数和排列数公式的运用,属于中档题。

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目






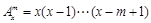 ,其中
,其中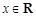 ,
,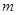 为正整数,且
为正整数,且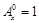 ,这是排列数
,这是排列数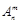 (
(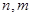 是正整数,且
是正整数,且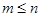 )的一种推广.
)的一种推广. 的值;
的值; ,②
,②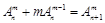 (其中
(其中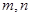 是正整数).是否都能推广到
是正整数).是否都能推广到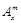 (
(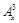 的单调区间.
的单调区间.