题目内容
(2012•天门模拟)下列命题中真命题的个数是( )
①“?x∈R,x2-x>0”的否定是“?x∈R,x2-x>0”;
②若|2x-1|>1,则0<
<1或
<0;
③S=
+
+
+…+
是奇数.
①“?x∈R,x2-x>0”的否定是“?x∈R,x2-x>0”;
②若|2x-1|>1,则0<
| 1 |
| x |
| 1 |
| x |
③S=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |
分析:①根据“?x∈R,结论p成立”的否定是“?x∈R,结论p的反面成立”可以判断出①的真假.
②由|x|>a>0,可得x>a或x<-a,即可求出x的范围.
③可用放缩法:一方面S<
+
<
<3,另一方面S>
+
+
+
=1,故可判断出③的真假.
②由|x|>a>0,可得x>a或x<-a,即可求出x的范围.
③可用放缩法:一方面S<
| 1 |
| 2 |
| 9 |
| 4 |
| 11 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
解答:解:①根据“?x∈R,结论p成立”的否定是“?x∈R,结论p的反面成立”可知:“?x∈R,x2-x>0”的否定
应是“?x∈R,x2-x≤0”.故①是假命题.
②由|2x-1|>1得:2x-1>1,或2x-1<-1,解得x>1,或x<0;由
<0或0<
<1,可解得x<0或x>1,因此②是真命题.
③一方面S<
+
<
<3,另一方面S>
+
+
+
=1,∴1<S<3,故S不可能是奇数.所以③是假命题.
综上可知只有②是真命题.
故选B.
应是“?x∈R,x2-x≤0”.故①是假命题.
②由|2x-1|>1得:2x-1>1,或2x-1<-1,解得x>1,或x<0;由
| 1 |
| x |
| 1 |
| x |
③一方面S<
| 1 |
| 2 |
| 9 |
| 4 |
| 11 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
综上可知只有②是真命题.
故选B.
点评:本题综合考查了命题的否定、含绝对值不等式及数列和的奇数偶数,准确掌握以上有关知识是解决问题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
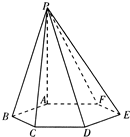 (2012•天门模拟)已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论正确的个数是( )
(2012•天门模拟)已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论正确的个数是( )