Question

（本小题满分10分）选修41：几何证明选讲

    如图，相交于A、B两点，AB是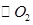的直径，过A点作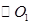的切线交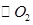于点E，并与BO₁的延长线交于点P，PB分别与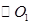、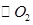交于C，D两点。

求证：（1）PA·PD=PE·PC；

      （2）AD=AE。

 

Answer 1

【答案】

见解析。

【解析】本试题主要是考查了平面几何中圆内的性质和三角形相似的性质的综合运用。

（1）由于利用题目总的切线和割线得到切割线定理的表达式，然后分析得到结论。

(2)结合第一问中的结论，以及圆的直径的性质，以及平行和垂直中包含角的相等关系，得到边的相等。

（Ⅰ）分别是⊙的割线∴      ①      （2分）

又分别是⊙的切线和割线∴  ②     （4分）

由①，②得                                （5分）

（Ⅱ）连结、

      设与相交于点

∵是⊙的直径

∴ 

∴是⊙的切线.  （6分）

由（Ⅰ）知，∴∥∴⊥,   （8分）

又∵是⊙的切线，∴

又，∴

∴                                                     （10分）