Question

已知函数f(x)=log₃(ax+b)的图象过点A(2,1)和B(5,2).

(1)求函数f(x)的解析式.

(2)记a_n=3^f(n),n∈N^*,是否存在正整数k,使得(1+)(1+)(1+)…(1+)≥k对一切n∈N^*均成立?若存在,求出k的最大值;若不存在,请说明理由.

Answer 1

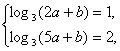解:(1)由得∴

∴f(x)=log₃(2x-1).

(2)a_n==2n-1,

1+=1+=,

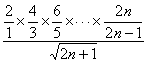×××…×≥k,

∴≥k.

    令g(n)=,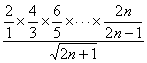

    则g(n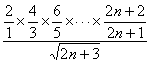+1)=,

∴=

=＞1.

∴{a_n}是递增数列.

∴g(n)_min=g(1)=≥k.

∴k≤.∴k的最大值为.

    又k为正整数,∴k最大为1.