题目内容
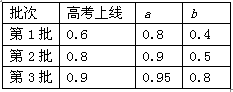
(本小题12分)在甲、乙两个盒子中分别装有标号为 的三个大小相同的球,现从甲、乙两个盒子中各取出
的三个大小相同的球,现从甲、乙两个盒子中各取出 个球,每个球被取出的可能性相等.
个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之和不小于 的概率.
的概率.
 的三个大小相同的球,现从甲、乙两个盒子中各取出
的三个大小相同的球,现从甲、乙两个盒子中各取出 个球,每个球被取出的可能性相等.
个球,每个球被取出的可能性相等.(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之和不小于
 的概率.
的概率. (1)取出的两个球上的标号为相同数字的概率为 .
.
(2)取出的两个球上标号之积能被3整除的概率为 .
.
 .
. (2)取出的两个球上标号之积能被3整除的概率为
 .
. 本题主要考查了等可能事件的概率公式的应用,解题的关键是准确求出每种情况下事件的个数.
(1)设从甲、乙两个盒子中各取1个球,其数字分别为x、y,,用(x,y)表示抽取结果,则所有可能的结果有9种,那么事件A包含的基本事件数为3,那么利用古典概型概率得到。
(2) 设“取出的两个球上标号的数字之和不小于4”为事件B,
则 事件B由7个基本事件组成,故所求概率
事件B由7个基本事件组成,故所求概率 .得到结论。
.得到结论。
解:设从甲、乙两个盒子中各取1个球,其数字分别为 ,
,
用 表示抽取结果,则所有可能的结果有9种,即
表示抽取结果,则所有可能的结果有9种,即
 ,
, ,
, ,
, ,
, ,
, ,,
,,
 ,
, ,
, .………………………4分
.………………………4分
(1)设“取出的两个球上的标号相同”为事件A,则 .
.
事件A由4个基本事件组成,故所求概率 .
.
答:取出的两个球上的标号为相同数字的概率为 . ………………8分
. ………………8分
(2)设“取出的两个球上标号的数字之和不小于4”为事件B,
则 .
.
事件B由7个基本事件组成,故所求概率 .
.
答:取出的两个球上标号之积能被3整除的概率为 . ………………12分
. ………………12分
(1)设从甲、乙两个盒子中各取1个球,其数字分别为x、y,,用(x,y)表示抽取结果,则所有可能的结果有9种,那么事件A包含的基本事件数为3,那么利用古典概型概率得到。
(2) 设“取出的两个球上标号的数字之和不小于4”为事件B,
则
 事件B由7个基本事件组成,故所求概率
事件B由7个基本事件组成,故所求概率 .得到结论。
.得到结论。解:设从甲、乙两个盒子中各取1个球,其数字分别为
 ,
,用
 表示抽取结果,则所有可能的结果有9种,即
表示抽取结果,则所有可能的结果有9种,即 ,
, ,
, ,
, ,
, ,
, ,,
,, ,
, ,
, .………………………4分
.………………………4分 (1)设“取出的两个球上的标号相同”为事件A,则
 .
. 事件A由4个基本事件组成,故所求概率
 .
.答:取出的两个球上的标号为相同数字的概率为
 . ………………8分
. ………………8分 (2)设“取出的两个球上标号的数字之和不小于4”为事件B,
则
 .
. 事件B由7个基本事件组成,故所求概率
 .
.答:取出的两个球上标号之积能被3整除的概率为
 . ………………12分
. ………………12分
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目

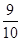
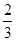
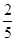
 张卡片(大小,形状都相同)上分别写有
张卡片(大小,形状都相同)上分别写有 ,
, ,
,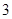 ,
, 外部的概率是 ( )
外部的概率是 ( )



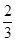 ,则
,则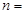 __________
__________