题目内容
（本小题共13分）
已知函数
R）．
（Ⅰ）求函数
的定义域，并讨论函数的单调性；
（Ⅱ）问是否存在实数
，使得函数在区间
上取得最小值3？请说明理由．
解：（Ⅰ）函数的定义域为
，且 
．
令
，得 
． ——————————————2分
当
时，
，
，函数在上是增函数；
当
时，在区间
上
，函数在上是减函数；
在区间
上
，函数在上是增函数．———6分
（Ⅱ）由（Ⅰ）知
，
（1）若
，则在区间上
，函数在上是增函数，
此时，取最小值
，
由
，得
；————————8分
（2）若
则在区间上
，函数在上是减函数，
此时，取最小值
，
由
，得
；———————10分
（3）若
，
则在区间
上，函数在上是减函数，
在区间上，函数在上是增函数，
此时，取最小值
，
由
，得
；——————12分
综上所述，存在实数
，使得在区间上取得最小值3．
——————————13分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的反函数为
，数列
和
满足：
，
，
的图象在点
处的切线在
轴上的截距为
．
}的通项公式；
的项仅
最小，求
的取值范围；
，数列
满足：
，且
，其中
．证明：
．
。
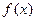的最小正周期：
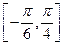上的最大值和最小值。
。
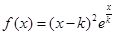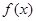的单调区间；
，都有
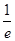，求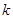
的取值范围。
：
，其中等于
的项有
个
，
，
.
，求
；
，求函数
的最小值.
，
为函数
的导函数． 
，求
的值；
，求函数
的单调区间．