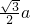Question

将锐角∠QMN=60°，边长MN=a的菱形MNPQ沿对角线NQ折成60°的二面角，则MP与NQ间的距离等于（　　）

• A．

  3

  2

  a
• B．

  3

  4

  a
• C．

  6

  4

  a
• D．

  3

  4

  a

Answer 1

分析：要求异面直线间的距离，关键是找（作）出它们的公垂线，根据菱形图形，合理运用二面角，从而得解

解答：解：作MO⊥QN于O点．则PO⊥QN．MO=PO=asin60°．△MNQ与△PNQ是60°的二面角．
PO在△PNQ内．MO在△MNQ内．即∠MOP为60°，
△MOP是边长为asin60°的等边三角形．
过O点作OD⊥PM于D点．OD即是MP与NQ间的距离．
OD=asin60°×sin60°=

3

4

a
故选B．

点评：本题的考点是与二面角有关的立体几何综合，考查图形的翻折，考查异面直线间的距离，应注意翻折前后图形的变与不变．