题目内容
解不等式: .
.
解:∵
故函数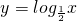 在区间(0,+∞)为减函数
在区间(0,+∞)为减函数
故原不等式可化为:
解得
故原不等式的解集为 .
.
分析:根据不等式两边均为以 为底的对数式,故我们可以根据函数
为底的对数式,故我们可以根据函数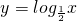 的单调性,将原不等式转化为一个关于x的一元二次不等式组来进行解答.
的单调性,将原不等式转化为一个关于x的一元二次不等式组来进行解答.
点评:本题考查的知识点是对数函数的单调性,对数函数的定义域,其中解答的关键是利用对数函数的单调性将问题转化为解一元二次不等式问题,解答时易忽略对数函数的真数比较大于0的原则,而错解为:{x|-3≤x≤0}

故函数
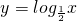 在区间(0,+∞)为减函数
在区间(0,+∞)为减函数故原不等式可化为:

解得

故原不等式的解集为
 .
.分析:根据不等式两边均为以
 为底的对数式,故我们可以根据函数
为底的对数式,故我们可以根据函数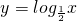 的单调性,将原不等式转化为一个关于x的一元二次不等式组来进行解答.
的单调性,将原不等式转化为一个关于x的一元二次不等式组来进行解答.点评:本题考查的知识点是对数函数的单调性,对数函数的定义域,其中解答的关键是利用对数函数的单调性将问题转化为解一元二次不等式问题,解答时易忽略对数函数的真数比较大于0的原则,而错解为:{x|-3≤x≤0}

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目