题目内容
设点P在△ABC内部及其边界上运动,并且
=x
+y
,则(x-1)2+(y-1)2的最小值为( )
| AP |
| AB |
| AC |
A、
| ||||
B、
| ||||
| C、1 | ||||
| D、2 |
分析:根据点P在△ABC内部及其边界上运动,并且
=x
+y
,可得
,(x-1)2+(y-1)2表示平面区域
,内的点(x,y)到点(1,1)的距离的平方,利用点到直线的距离公式,可求(x-1)2+(y-1)2的最小值.
| AP |
| AB |
| AC |
|
|
解答: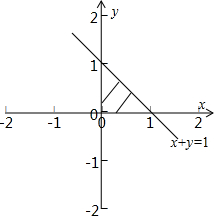 解:∵点P在△ABC内部及其边界上运动,并且
解:∵点P在△ABC内部及其边界上运动,并且
=x
+y
,
∴
,
∵在直角坐标系x0y内,(x-1)2+(y-1)2表示平面区域
,内的点(x,y)到点(1,1)的距离的平方.
∴数形结合知(1,1)到直线x+y=1的距离最小,此时d=
,
∴(x-1)2+(y-1)2的最小值为
故选:B.
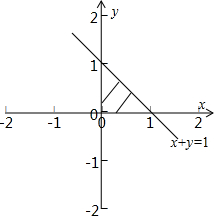 解:∵点P在△ABC内部及其边界上运动,并且
解:∵点P在△ABC内部及其边界上运动,并且| AP |
| AB |
| AC |
∴
|
∵在直角坐标系x0y内,(x-1)2+(y-1)2表示平面区域
|
∴数形结合知(1,1)到直线x+y=1的距离最小,此时d=
| 1 | ||
|
∴(x-1)2+(y-1)2的最小值为
| 1 |
| 2 |
故选:B.
点评:本题考查线性规划知识的运用,考查数形结合的数学思想,考查学生的计算能力,正确确定可行域是关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目