题目内容
已知函数f(x)=(1)当|a|≤![]() 时,求证:f(x)在(-1,1)内是减函数;
时,求证:f(x)在(-1,1)内是减函数;
(2)若函数y=f(x)在区间(-1,1)内有且只有一个极值点,求a的取值范围.
解:(1)∵f′(x)=2x2-4ax-3,且|a|≤![]() ,
,
∴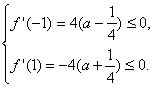
又函数f′(x)图象的对称轴x=a,a∈(-1,1),
∴在区间(-1,1)内,恒有f′(x)<0.
故f(x)在(-1,1)内是减函数.
(2)设极值点为x0(-1<x0<1),则f′(x0)=0.
当a>![]() 时,
时,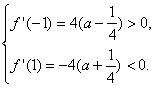
∴在(-1,x0)内f′(x)>0,在(x0,1)内f′(x)<0,即f(x)在(-1,x0)内是增函数,在(x0,1)内是减函数.
∴当a>![]() 时,f(x)在(-1,1)内有且只有一个极大值点.
时,f(x)在(-1,1)内有且只有一个极大值点.
当a<![]() 时,同理可知,f(x)在(-1,1)内有且只有一个极小值点.
时,同理可知,f(x)在(-1,1)内有且只有一个极小值点.
当![]() ≤a≤
≤a≤![]() 时,由(1)可知,f(x)在(-1,1)内没有极值点.
时,由(1)可知,f(x)在(-1,1)内没有极值点.
故所求a的取值范围是(-∞,![]() )∪(
)∪(![]() ,+∞).
,+∞).

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目