题目内容
函数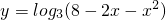 的定义域为A,值域为B,求A∩B.
的定义域为A,值域为B,求A∩B.
解:∵8-2x-x2>0,(x+4)(x-2)<0
∴-4<x<2,
∴A=(-4,2)…(4分)
令t=8-2x-x2=-(x+1)2+9,则y=log3t,(0<t≤9),
由对数函数的图象可知,B=(-∞,2]…(8分)
∴A∩B=(-4,2)…(12分)
分析:由8-2x-x2>0,(x+4)(x-2)<0,知A=(-4,2).令t=8-2x-x2=-(x+1)2+9,则y=log3t,(0<t≤9),由对数函数的图象可知,B=(-∞,2],由此能求出A∩B.
点评:本题考查对数的定义域和交集及其运算,是基础题.解题时要认真审题,仔细解答.
∴-4<x<2,
∴A=(-4,2)…(4分)
令t=8-2x-x2=-(x+1)2+9,则y=log3t,(0<t≤9),
由对数函数的图象可知,B=(-∞,2]…(8分)
∴A∩B=(-4,2)…(12分)
分析:由8-2x-x2>0,(x+4)(x-2)<0,知A=(-4,2).令t=8-2x-x2=-(x+1)2+9,则y=log3t,(0<t≤9),由对数函数的图象可知,B=(-∞,2],由此能求出A∩B.
点评:本题考查对数的定义域和交集及其运算,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
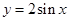 的定义域为[a,b],值域为[-2,1],则
的定义域为[a,b],值域为[-2,1],则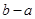 的值不可能是 ( )
的值不可能是 ( )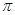 B.
B.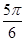 C.
C.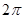 D.
D.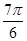
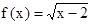 的定义域为A,函数
的定义域为A,函数 的值域为B。
的值域为B。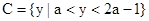 ,且
,且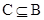 ,求实数a的取值范围。
,求实数a的取值范围。 的定义域为A,
的定义域为A,
 的定义域为B.
的定义域为B. ,求实数
,求实数 的取值范围.
的取值范围.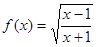 的定义域为A, 函数
的定义域为A, 函数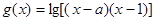 (其中
(其中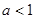 )的定义域为B.
)的定义域为B. 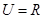 ,当a=0时,求
,当a=0时,求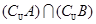 ;
;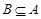 , 求实数
, 求实数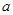 的取值范围.
的取值范围.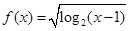 的定义域为A,函数
的定义域为A,函数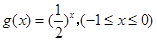 的值域为B.
的值域为B. ;
;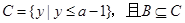 ,求
,求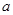 的取值范围
的取值范围