Question

已知正方体ABCD-A₁B₁C₁D₁中，E为棱CC₁的中点．如果一只蜜蜂在正方体ABC-A₁B₁C₁D₁内部任意飞，则它飞入三棱锥A₁-BDE内部的概率为（　　）

• A．

  1

  4

• B．

  1

  3

• C．

  1

  2

• D．

  2

  5

Answer 1

分析：由已知中正方体ABCD-A₁B₁C₁D₁中，E为棱CC₁的中点．如果一只蜜蜂在正方体ABC-A₁B₁C₁D₁内部任意飞，我们设正方体ABCD-A₁B₁C₁D₁的棱长为2，分别计算出正方体的体积及棱锥的体积，代入几何概型概率公式，即可得到答案．

解答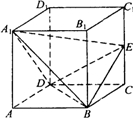：解：设正方体ABCD-A₁B₁C₁D₁的棱长为2，则
V_正方体=8
又∵E为棱CC₁的中点，
则BD=A₁B=A₁D=2

2

，BE=DE=

5

，A₁E=3，
设AC与BD交于点O，连接A₁0，EO，则EO=

3

，A₁O=

6

由勾股定理，易得EO⊥A₁O，又∵A₁O⊥BD，EO∩BD=O
∴A₁O⊥平面BDE，即A₁O为三棱锥A₁-BDE高
∴VA1-BDE=

1

3

•SBDE•A1O=2
则它飞入三棱锥A₁-BDE内部的概率P=

1

4

故选A

点评：本题考查的知识点是几何概型，其中根据已知计算出正方体的体积及棱锥的体积是解答本题的关键．