题目内容
已知集合A={a，b，c}，B={1，2，3}，映射f：A→B满足f（a）+f（b）+f（c）=7，则这样的映射个数为（ ）
分析：由已知集合A={a，b，c}，B={1，2，3}，映射f：A→B满足f（a）+f（b）+f（c）=7，我们用列举法，求出所有满足条件的情况，即可得到答案．
解答：解：∵集合A={a，b，c}，B={1，2，3}，映射f：A→B，
则记f（a），f（b），f（c）对应的函数值分别为（m，n，p），则满足条件m+n+p=7情况共有：
（2，2，3），（2，3，2），（3，2，2），（1，3，3），（3，1，3），（3，3，1）；
这样的映射共六个，
故选D．
则记f（a），f（b），f（c）对应的函数值分别为（m，n，p），则满足条件m+n+p=7情况共有：
（2，2，3），（2，3，2），（3，2，2），（1，3，3），（3，1，3），（3，3，1）；
这样的映射共六个，
故选D．
点评：本题考查的知识点是映射的定义，正确理解映射的定义，按照一定的规则，对所有情况进行列举，是解答本题的关键．
练习册系列答案
相关题目
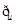B)＝R，则实数a的取值范围是 ( )