题目内容
函数f（x）=
，若直线y=kx-1与函数y=f（x）有3个公共点，则实数k的取值范围是________．
（0，1）
分析：要求满足直线y=kx-1与函数y=f（x）有3个公共点时，实数k的取值范围，我们可以画出直线y=kx-1与曲线y═f（x）图象，有且仅有三个交点时实数k的取值．
解答：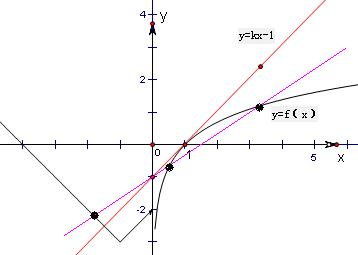
解：直线y=kx-1与曲线y=f（x）的图象如图所示，
由图可知直线y=kx-1与曲线y=f（x）．
当k=1时，有且仅有两个交点，
当0＜k＜1时时，直线y=kx-1与曲线y=f（x）有3个公共点，
实数k的取值范围是（0，1）
故答案为：（0，1）
．
点评：本题考查的知识点是根的存在性及根的个数判断，画出函数的图象，进而利用图象法进行解答是解答本题的关键．
分析：要求满足直线y=kx-1与函数y=f（x）有3个公共点时，实数k的取值范围，我们可以画出直线y=kx-1与曲线y═f（x）图象，有且仅有三个交点时实数k的取值．
解答：
解：直线y=kx-1与曲线y=f（x）的图象如图所示，由图可知直线y=kx-1与曲线y=f（x）．
当k=1时，有且仅有两个交点，
当0＜k＜1时时，直线y=kx-1与曲线y=f（x）有3个公共点，
实数k的取值范围是（0，1）
故答案为：（0，1）
．
点评：本题考查的知识点是根的存在性及根的个数判断，画出函数的图象，进而利用图象法进行解答是解答本题的关键．
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、命题：“已知函数f（x），若f（x+1）与f（x-1）均为奇函数，则f（x）为奇函数，”为直命题 | B、“x＞1”是“|x|＞1”的必要不充分条件 | C、若“p且q”为假命题，则p，q均为假命题 | D、命题p：”?x∈R，使得x2+x+1＜0”，则?p：”?x∈R，均有x2+x+1≥0” |