题目内容
已知椭圆的中心在原点,焦点在x轴上,离心率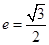 。它有一个顶点恰好是抛物线
。它有一个顶点恰好是抛物线 =4y的焦点。过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且
=4y的焦点。过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且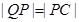 。
。
(Ⅰ)求动点C的轨迹E的方程;
(Ⅱ)设椭圆的左右顶点分别为A,B,直线AC(C点不同于A,B)与直线 交于点R,D为线段RB的中点。试判断直线CD与曲线E的位置关系,并证明你的结论。
交于点R,D为线段RB的中点。试判断直线CD与曲线E的位置关系,并证明你的结论。
(Ⅰ)动点 的轨迹
的轨迹 的方程为
的方程为 ;(Ⅱ)直线
;(Ⅱ)直线 与圆
与圆 相切.
相切.
解析试题分析:(Ⅰ)求动点C的轨迹E的方程,由题意首先求出椭圆的方程为 ,设
,设 ,
, ,由已知
,由已知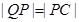 ,找出
,找出 与
与 之间的关系,利用点
之间的关系,利用点 在椭圆
在椭圆 上,代入即可求出动点C的轨迹E的方程;(Ⅱ)判断直线CD与曲线E的位置关系,由(Ⅰ)动点
上,代入即可求出动点C的轨迹E的方程;(Ⅱ)判断直线CD与曲线E的位置关系,由(Ⅰ)动点 的轨迹
的轨迹 的方程为
的方程为 ,主要看圆心到直线距离与半径之间的关系,因此,主要找直线
,主要看圆心到直线距离与半径之间的关系,因此,主要找直线 的方程,设
的方程,设 ,则
,则 ,由题意
,由题意 三点共线,得
三点共线,得  ∥
∥ ,设点
,设点 的坐标为
的坐标为 ,利用共线,求出
,利用共线,求出 ,得点
,得点 的坐标为
的坐标为 ,从而得点
,从而得点 的坐标为
的坐标为 ,这样写出直线
,这样写出直线 的方程,利用点到直线位置关系,从而可判断直线CD与曲线E的位置关系.
的方程,利用点到直线位置关系,从而可判断直线CD与曲线E的位置关系.
试题解析:(Ⅰ)设椭圆C的方程为 ,则由题意知b = 1,
,则由题意知b = 1, ,
,
∴ ,
, ,所以椭圆的方程为
,所以椭圆的方程为 。(2分)
。(2分)
设 ,
, ,由题意得
,由题意得 ,即
,即
又 ,代入得
,代入得 ,即
,即 。
。
即动点 的轨迹
的轨迹 的方程为
的方程为 。(6分)
。(6分)
(Ⅱ)设 ,点
,点 的坐标为
的坐标为 ,
,
∵ 三点共线,∴
三点共线,∴  ∥
∥ ,
,
而 ,
, ,则
,则 ,∴
,∴ ,
,
∴点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,
,
∴直线 的斜率为
的斜率为 ,(9分)
,(9分)
而 ,∴
,∴ ,∴
,∴ ,
,
∴直线 的方程为
的方程为 ,化简得
,化简得 ,
,
∴圆心 到直线
到直线 的距离
的距离 ,
,
所以直线 与圆
与圆 相切。(13分)
相切。(13分)
考点:求轨迹方程,判断直线与圆的位置关系.

练习册系列答案
相关题目
 )作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4.
)作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4. =
= +
+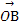 ,求|
,求| (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点. 的三个顶点
的三个顶点 ,
, ,
, ,其外接圆为
,其外接圆为 .
. 过点
过点 ,且被
,且被 上的任意一点
上的任意一点 ,若在以
,若在以 ,使得点
,使得点 是线段
是线段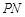 的中点,求
的中点,求 的半径
的半径 的取值范围.
的取值范围. 的左右顶点分别为
的左右顶点分别为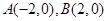 ,离心率
,离心率 .过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且
.过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且 .
. 交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.
交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论. .(14分)
.(14分) (O为坐标原点),求m的值;
(O为坐标原点),求m的值; 为直径的圆的方程.
为直径的圆的方程. 经过
经过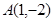 ,
,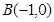 两点,且在两坐标轴上的四个截距之和为2.
两点,且在两坐标轴上的四个截距之和为2. 为圆内一点,求经过点
为圆内一点,求经过点 被圆
被圆 的方程.
的方程. 中,点
中,点 ,直线
,直线 。设圆
。设圆 的半径为
的半径为 ,圆心在
,圆心在 上。
上。
 上,过点
上,过点 作圆
作圆 ,使
,使 ,求圆心
,求圆心 的取值范围。.
的取值范围。.