题目内容
设曲线Cn:f(x)=xn+1(n∈N*)在点P(-| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求数列{yn}的通项公式;
(Ⅱ)设数列{yn}的前n项和为Sn,猜测Sn的最大值并证明你的结论.
分析:(I)欲求数列{yn}的通项公式,只须求出切线与y轴的交点坐标即可,故先利用导数求出在x=-
处的导函数值,再结合导数的几何意义即可求出切线的斜率进而求出切线方程最后得到与y轴交点坐标.从而问题解决.
(II)根据所求数列的特点,采用错位相消法求出数列{yn}的前n项和为Sn,再算出它的前几项观察此数列的最大值,最后对n进行分类讨论:当n为奇数时;当n为偶数时.进行证明即可.
| 1 |
| 2 |
(II)根据所求数列的特点,采用错位相消法求出数列{yn}的前n项和为Sn,再算出它的前几项观察此数列的最大值,最后对n进行分类讨论:当n为奇数时;当n为偶数时.进行证明即可.
解答:解:(Ⅰ)∵f′(x)=(n+1)xn(n∈N*),(1分)
∴点P处的切线斜率kn=(n+1)(-
)n,(2分)
∴切线方程为:y-(-
)n+1=(n+1)(-
)n(x+
),(3分)
令x=0得:yn=(-
)n+1+
•(-
)n,
故数列{yn}的通项公式为:yn=
•(-
)n.(4分)
(Ⅱ)Sn=
•(-
)+
•(-
)2+
•(-
)3++
•(-
)n①
两边同乘-
得:-
•Sn=
•(-
)2+
•(-
)3+
•(-
)4++
•(-
)n+1②
∴得:
•sn=
•(-
)+
•(-
)2+
•(-
)3++
•(-
)n-
•(-
)n+1(6分)
∴3Sn=(-
)+(-
)2+(-
)3++(-
)n-n•(-
)n+1
=
-n•(-
)n+1
=-
-n•(-
)n+1
∴Sn=
[
•(-
)n-1](8分)
其中S1=y1=-
,S2=y1+y2=0,S3=-
,S4=-
猜测Sn的最大值为S2=0.证明如下:(10分)
(i)当n为奇数时,Sn=-
[
•(
)n+1]<0;(11分)
(ii)当n为偶数时,Sn=
•(
-1),
设h(n)=
,则h(n+2)=
.
h(n+2)-h(n)=
-
=-
<0,
∴h(n+2)<h(n).(13分)
故h(n)=
的最大值为h(2)=1,即Sn的最大值为S2=0.(14分)
解法2(Ⅱ)任意k∈N*,都有y2k-1<0,y2k>0;
所以Sn的最大值就是S2k的最大值.
令ak=y2k-1+y2k=
,显然a1=0,k>1,ak<0,
所以S2k=a1+a2++ak的最大值是S2=a1=0.
∴点P处的切线斜率kn=(n+1)(-
| 1 |
| 2 |
∴切线方程为:y-(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令x=0得:yn=(-
| 1 |
| 2 |
| n+1 |
| 2 |
| 1 |
| 2 |
故数列{yn}的通项公式为:yn=
| n |
| 2 |
| 1 |
| 2 |
(Ⅱ)Sn=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
两边同乘-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
∴得:
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
∴3Sn=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
-
| ||||
1+
|
| 1 |
| 2 |
=-
1-(-
| ||
| 3 |
| 1 |
| 2 |
∴Sn=
| 1 |
| 9 |
| 2+3n |
| 2 |
| 1 |
| 2 |
其中S1=y1=-
| 1 |
| 4 |
| 3 |
| 16 |
| 1 |
| 16 |
猜测Sn的最大值为S2=0.证明如下:(10分)
(i)当n为奇数时,Sn=-
| 1 |
| 9 |
| 2+3n |
| 2 |
| 1 |
| 2 |
(ii)当n为偶数时,Sn=
| 1 |
| 9 |
| 2+3n |
| 2n+1 |
设h(n)=
| 2+3n |
| 2n+1 |
| 8+3n |
| 2n+3 |
h(n+2)-h(n)=
| 8+3n |
| 2n+3 |
| 2+3n |
| 2n+1 |
| 9n |
| 2n+3 |
∴h(n+2)<h(n).(13分)
故h(n)=
| 2+3n |
| 2n+1 |
解法2(Ⅱ)任意k∈N*,都有y2k-1<0,y2k>0;
所以Sn的最大值就是S2k的最大值.
令ak=y2k-1+y2k=
| 1-k |
| 4k |
所以S2k=a1+a2++ak的最大值是S2=a1=0.
点评:本小题主要考查利用导数研究曲线上某点切线方程、数列的求和、数列递推式等基础知识,考查运算求解能力、化归与转化思想.属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
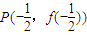 处的切线与y轴交于点Qn(0,yn).
处的切线与y轴交于点Qn(0,yn).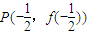 处的切线与y轴交于点Qn(0,yn).
处的切线与y轴交于点Qn(0,yn).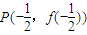 处的切线与y轴交于点Qn(0,yn).
处的切线与y轴交于点Qn(0,yn).