题目内容
设函数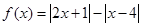 .
.
(I)解不等式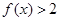 ;
;
(II)求函数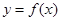 的最小值.
的最小值.
(Ⅰ)  ;(Ⅱ)
;(Ⅱ)  .
.
解析试题分析:(Ⅰ)先将函数 写成分段函数的形式,根据分段函数的解析式作出函数的图像,然后求出直线
写成分段函数的形式,根据分段函数的解析式作出函数的图像,然后求出直线 与函数图像的交点坐标为
与函数图像的交点坐标为 和
和 ,利用数形结合的思想可知
,利用数形结合的思想可知 的解集;(Ⅱ)找到函数图像的最低点,求出最低点的纵坐标即可.
的解集;(Ⅱ)找到函数图像的最低点,求出最低点的纵坐标即可.
试题解析:(Ⅰ)令 ,则有
,则有 ,
,
则作出函数 的图像如下:
的图像如下:
它与直线 的交点为
的交点为 和
和 .
.
所以 的解集为:
的解集为: . 6分
. 6分
(Ⅱ)由函数 的图像可知,
的图像可知,
当 时,函数
时,函数 取得最小值
取得最小值 . 10分
. 10分
考点:1.分段函数的解析式及其图像;2.绝对值不等式;3.数形结合思想

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
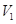 .
.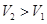 吗?若能、给出你的一种设计方案。
吗?若能、给出你的一种设计方案。  千米的速度匀速行驶130千米
千米的速度匀速行驶130千米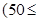
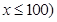 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.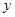 关于
关于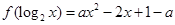 ,
,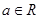 .
.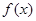 的解析式;
的解析式;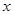 的方程
的方程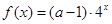
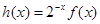 ,
,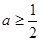 时,对任意
时,对任意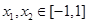 总有
总有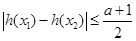 成立,求
成立,求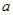 的取值范围.
的取值范围. 是定义在
是定义在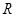 上的奇函数,当
上的奇函数,当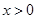 时的解析式为
时的解析式为 .
.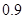 万元,年维修费用第一年是
万元,年维修费用第一年是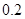 万元,第二年是
万元,第二年是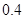 万元,第三年是
万元,第三年是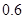 万元,…,以后逐年递增
万元,…,以后逐年递增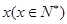 年的维修费用的和为
年的维修费用的和为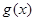 ,年平均费用为
,年平均费用为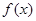 .
.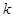 米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为
米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为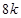 元/根,且当两相邻的座位之间的圆弧长为
元/根,且当两相邻的座位之间的圆弧长为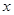 米时,相邻两座位之间的钢管和其中一个座位的总费用为
米时,相邻两座位之间的钢管和其中一个座位的总费用为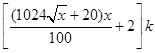 元.假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为
元.假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为 元.
元.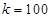 米时,试确定座位的个数,使得总造价最低?
米时,试确定座位的个数,使得总造价最低?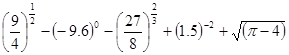 ;
;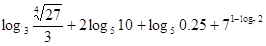 .
.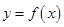 和
和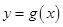 的图象关于
的图象关于 轴对称,且
轴对称,且 .
.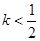 时,解不等式
时,解不等式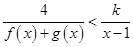 .
.