题目内容
已知函数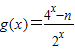 是奇函数,
是奇函数,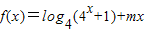 是偶函数.
是偶函数.(1)求m+n的值;
(2)设
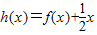 ,若g(x)>h[log4(2a+1)]对任意x≥1恒成立,求实数a的取值范围.
,若g(x)>h[log4(2a+1)]对任意x≥1恒成立,求实数a的取值范围.
【答案】分析:(1)由g(x)为定义在R上的奇函数,得g(0)=0,解得n=1;再根据偶函数满足f(-x)=f(x),比较系数可得m=- ,由此即可得到m+n的值.
,由此即可得到m+n的值.
(2)由(1)得h(x)=log4(4x+1),易得h[log4(2a+1)]=log4(2a+2).而定义在R上的增函数g(x)在x≥1时的最小值为g(1)= ,从而不等式转化成
,从而不等式转化成 >log4(2a+2),由此再结合真数必须大于0,不难解出实数a的取值范围.
>log4(2a+2),由此再结合真数必须大于0,不难解出实数a的取值范围.
解答:解:(1)由于g(x)为奇函数,且定义域为R,
∴g(0)=0,即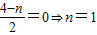 ,…(3分)
,…(3分)
∵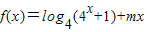 ,
,
∴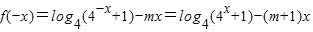 ,
,
∵f(x)是偶函数,
∴f(-x)=f(x),得mx=-(m+1)x恒成立,故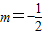 ,
,
综上所述,可得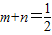 ;…(4分)
;…(4分)
(2)∵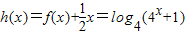 ,
,
∴h[log4(2a+1)]=log4(2a+2),…(2分)
又∵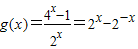 在区间[1,+∞)上是增函数,
在区间[1,+∞)上是增函数,
∴当x≥1时,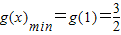 …(3分)
…(3分)
由题意,得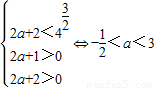 ,
,
因此,实数a的取值范围是: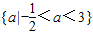 .…(3分)
.…(3分)
点评:本题给出含有指数和对数形式的函数,在已知奇偶性的情况下求参数m、n的值,并讨论不等式恒成立的问题,着重考查了对数函数图象与性质的综合应用、函数的奇偶性和不等式恒成立等知识点,属于中档题.
 ,由此即可得到m+n的值.
,由此即可得到m+n的值.(2)由(1)得h(x)=log4(4x+1),易得h[log4(2a+1)]=log4(2a+2).而定义在R上的增函数g(x)在x≥1时的最小值为g(1)=
 ,从而不等式转化成
,从而不等式转化成 >log4(2a+2),由此再结合真数必须大于0,不难解出实数a的取值范围.
>log4(2a+2),由此再结合真数必须大于0,不难解出实数a的取值范围.解答:解:(1)由于g(x)为奇函数,且定义域为R,
∴g(0)=0,即
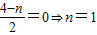 ,…(3分)
,…(3分)∵
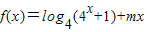 ,
,∴
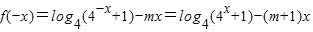 ,
,∵f(x)是偶函数,
∴f(-x)=f(x),得mx=-(m+1)x恒成立,故
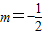 ,
,综上所述,可得
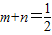 ;…(4分)
;…(4分)(2)∵
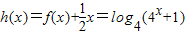 ,
,∴h[log4(2a+1)]=log4(2a+2),…(2分)
又∵
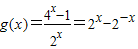 在区间[1,+∞)上是增函数,
在区间[1,+∞)上是增函数,∴当x≥1时,
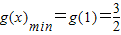 …(3分)
…(3分)由题意,得
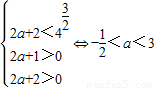 ,
,因此,实数a的取值范围是:
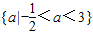 .…(3分)
.…(3分)点评:本题给出含有指数和对数形式的函数,在已知奇偶性的情况下求参数m、n的值,并讨论不等式恒成立的问题,着重考查了对数函数图象与性质的综合应用、函数的奇偶性和不等式恒成立等知识点,属于中档题.

练习册系列答案
相关题目
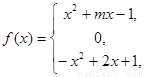
 是奇函数.
是奇函数.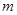 的值;
的值; 在区间
在区间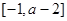 上单调递增,求实数
上单调递增,求实数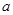 的取值范围;
的取值范围; 是奇函数且是
是奇函数且是 上的增函数,若
上的增函数,若 满足不等式
满足不等式 ,则
,则 的最大值是( )
的最大值是( ) B.
B. C.
C. D.
D.
 是奇函数,
是奇函数, 是偶函数。
是偶函数。 的值;
的值; 若
若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 是奇函数,
是奇函数, 是偶函数。(1)求
是偶函数。(1)求 的值;(2)设
的值;(2)设 若
若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 是奇函数,
是奇函数, 是偶函数。
是偶函数。 的值;
的值; 若
若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。