题目内容
如图1,在Rt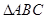 中,
中,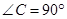 ,
,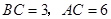 ,D、E分别是
,D、E分别是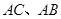 上的点,且
上的点,且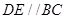 ,将
,将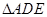 沿
沿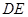 折起到
折起到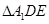 的位置,使
的位置,使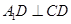 ,如图2.
,如图2.
(Ⅰ)求证:平面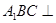 平面
平面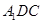 ;
;
(Ⅱ)若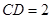 ,求
,求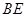 与平面
与平面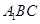 所成角的余弦值;
所成角的余弦值;
(Ⅲ)当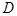 点在何处时,
点在何处时,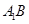 的长度最小,并求出最小值.
的长度最小,并求出最小值.
【答案】
(1)根据面面垂直的判定定理,结合线面 平面
平面 得到证明。
得到证明。
(2)  (3)
(3) 
【解析】
试题分析:解:(Ⅰ)证明:在△ 中,
中,
 .又
.又

 平面
平面 .
.
又
 平面
平面 ,又
,又 平面
平面 ,
,
故平面 平面
平面 …4分)
…4分)
(Ⅱ)由(1)知
故以D为原点,  分别为x,y,z轴建立直角坐标系.
分别为x,y,z轴建立直角坐标系.
因为CD="2,"
则 …(5分)
…(5分)
 ,设平面
,设平面 的一个法向量为
的一个法向量为
则 取法向量
取法向量 ,则直线BE与平面
,则直线BE与平面 所成角
所成角 ,
,

 (8分)
(8分)
故直线BE与平面 所成角的余弦值为
所成角的余弦值为 . (9分)
. (9分)
(Ⅲ)设 ,则
,则 ,则
,则 ,
,
 ,则当
,则当 时
时 最大为
最大为 .
…(12分)
.
…(12分)
考点:空间中的垂直和角的求解
点评:解决的关键是利用向量的方法结合法向量以及直线的方向向量来表示角和距离,属于基础题。

练习册系列答案
相关题目
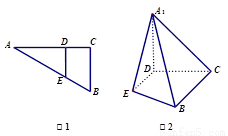
 (2012•北京)如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(2012•北京)如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2. 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6.D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6.D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2.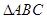 中,
中, 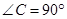 ,
,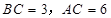 .D、E分别是
.D、E分别是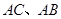 上的点,且
上的点,且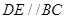 .将
.将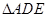 沿
沿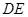 折起到
折起到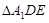 的位置,使
的位置,使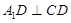 ,如图2.
,如图2.
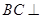 平面
平面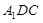 ;
;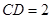 ,求
,求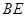 与平面
与平面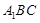 所成角的正弦值;
所成角的正弦值; 中,
中,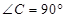 ,
,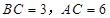 .D、E分别是
.D、E分别是 上的点,且
上的点,且 ,将
,将 沿
沿 折起到
折起到 的位置,使
的位置,使 ,如图2.
,如图2.
 平面
平面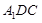 ;
; ,求
,求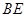 与平面
与平面 所成角的余弦值;
所成角的余弦值; 点在何处时,
点在何处时, 的长度最小,并求出最小值.
的长度最小,并求出最小值.