题目内容
将函数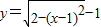 (x∈[0,2])图象绕原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则a的最大值是( )
(x∈[0,2])图象绕原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则a的最大值是( )A.
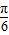
B.
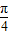
C.
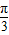
D.
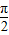
【答案】分析:确定函数在x=0处,函数图象的切线斜率,可得倾斜角,从而可得结论.
解答:解:由题意,函数图象如图所示, 函数在[0,1]上为增函数,在[1,2]上为减函数.
函数在[0,1]上为增函数,在[1,2]上为减函数.
设函数在x=0 处,切线斜率为k,则k=f'(0)
∵f'(x)= •
• ,
,
∴∴k=f'(0)=1,可得切线的倾斜角为45°,
因此,要使旋转后的图象仍为一个函数的图象,旋转θ后的切线倾斜角最多为 90°,也就是说,最大旋转角为90°-45°=45°,即θ的最大值为45°
故选B.
点评:本题考查了导数的几何意义和函数的图象与图象变化等知识点,将函数图象绕原点逆时针旋转θ后,所得曲线仍是一个函数的图象,求角θ的最大值,属于中档题.
解答:解:由题意,函数图象如图所示,
 函数在[0,1]上为增函数,在[1,2]上为减函数.
函数在[0,1]上为增函数,在[1,2]上为减函数.设函数在x=0 处,切线斜率为k,则k=f'(0)
∵f'(x)=
 •
• ,
,∴∴k=f'(0)=1,可得切线的倾斜角为45°,
因此,要使旋转后的图象仍为一个函数的图象,旋转θ后的切线倾斜角最多为 90°,也就是说,最大旋转角为90°-45°=45°,即θ的最大值为45°
故选B.
点评:本题考查了导数的几何意义和函数的图象与图象变化等知识点,将函数图象绕原点逆时针旋转θ后,所得曲线仍是一个函数的图象,求角θ的最大值,属于中档题.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
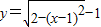 (x∈[0,2])图象绕原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则a的最大值是( )
(x∈[0,2])图象绕原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则a的最大值是( )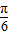
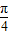
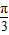
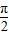
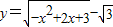 (x∈[0,2])的图象绕坐标原点逆时针旋转θ(θ为锐角),若所得曲线仍是一个函数的图象,则θ的最大值为 .
(x∈[0,2])的图象绕坐标原点逆时针旋转θ(θ为锐角),若所得曲线仍是一个函数的图象,则θ的最大值为 .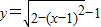 (x∈[0,2])图象绕原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则a的最大值是( )
(x∈[0,2])图象绕原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则a的最大值是( )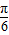
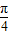
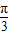
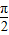
 (x∈[0,2])的图象绕坐标原点逆时针旋转θ(θ为锐角),若所得曲线仍是一个函数的图象,则θ的最大值为 .
(x∈[0,2])的图象绕坐标原点逆时针旋转θ(θ为锐角),若所得曲线仍是一个函数的图象,则θ的最大值为 .