题目内容
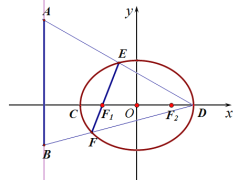
【题目】如图,C、D是离心率为![]() 的椭圆的左、右顶点,
的椭圆的左、右顶点,![]() 、
、![]() 是该椭圆的左、右焦点, A、B是直线
是该椭圆的左、右焦点, A、B是直线![]() 4上两个动点,连接AD和BD,它们分别与椭圆交于点E、F两点,且线段EF恰好过椭圆的左焦点
4上两个动点,连接AD和BD,它们分别与椭圆交于点E、F两点,且线段EF恰好过椭圆的左焦点![]() . 当
. 当![]() 时,点E恰为线段AD的中点.
时,点E恰为线段AD的中点.
(Ⅰ)求椭圆的方程;
(Ⅱ)求证:以AB为直径的圆始终与直线EF相切.
【答案】(Ⅰ)![]() (Ⅱ)见证明
(Ⅱ)见证明
【解析】
(Ⅰ)由题意可得![]() ,结合
,结合![]() 可求出
可求出![]() ,进而可求得椭圆的方程;(Ⅱ)设EF的方程为:
,进而可求得椭圆的方程;(Ⅱ)设EF的方程为:![]() ,E(
,E(![]() )、F(
)、F(![]() ),与椭圆联立,运用韦达定理得
),与椭圆联立,运用韦达定理得![]() ,
,![]() ,又设
,又设![]() ,由三点共线得
,由三点共线得![]() ,
,![]() ,求出
,求出![]() 中点
中点![]() 坐标
坐标![]() ,求出点M到直线EF的距离
,求出点M到直线EF的距离![]() ,进而证得结果.
,进而证得结果.
(Ⅰ)∵当![]() 时,点E恰为线段AD的中点,
时,点E恰为线段AD的中点,
∴![]() ,又
,又![]() ,联立解得:
,联立解得:![]() ,
,![]() ,
,![]() ,
,
∴椭圆的方程为![]() .
.
(Ⅱ)设EF的方程为:![]() ,E(
,E(![]() )、F(
)、F(![]() ),
),
 联立得:
联立得:![]()
∴![]() ,
,
∴ ……(*)
……(*)
又设![]() ,由A、E、D三点共线得
,由A、E、D三点共线得![]() ,同理可得
,同理可得![]() .
.
 ,
,
∴ .
.
设AB中点为M,则M坐标为(![]() )即(
)即(![]()
![]() ),
),
∴点M到直线EF的距离![]() .
.
故以AB为直径的圆始终与直线EF相切.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
【题目】在第十五次全国国民阅读调查中,某地区调查组获得一个容量为![]() 的样本,其中城镇居民
的样本,其中城镇居民![]() 人,农村居民
人,农村居民![]() 人.在这些居民中,经常阅读的城镇居民
人.在这些居民中,经常阅读的城镇居民![]() 人,农村居民
人,农村居民![]() 人.
人.
(Ⅰ)填写下面列联表,并判断是否有![]() 的把握认为,经常阅读与居民居住地有关?
的把握认为,经常阅读与居民居住地有关?
城镇居民 | 农村居民 | 合计 | |
经常阅读 |
|
| |
不经常阅读 | |||
合计 |
|
(Ⅱ)从该地区居民城镇的居民中,随机抽取![]() 位居民参加一次阅读交流活动,记这
位居民参加一次阅读交流活动,记这![]() 位居民中经常阅读的人数为
位居民中经常阅读的人数为![]() ,若用样本的频率作为概率,求随机变量
,若用样本的频率作为概率,求随机变量![]() 的分布列和期望.
的分布列和期望.
附: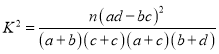 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|