ÌâÄṡÄÚÈÝ
ÔÚÆẄÃæÖḟẄÇṪøḟêÏṁxoyÉÏ£Ỳẁø¶ẀÅṪÎïÏßL£ẃy= x2£®ÊṁÊýp£ỲqÂúṪãp2-4qḂÝ0£Ỳx1£Ỳx2ÊÇṖẄġÌx2-px+q=0ṁÄÁẄẁù£ỲỳÇḊÕ£Ẁp£Ỳq£©=max{|x1|£Ỳ|x2|}£®
x2£®ÊṁÊýp£ỲqÂúṪãp2-4qḂÝ0£Ỳx1£Ỳx2ÊÇṖẄġÌx2-px+q=0ṁÄÁẄẁù£ỲỳÇḊÕ£Ẁp£Ỳq£©=max{|x1|£Ỳ|x2|}£®£Ẁ1£©ṗýṁã£ỲA£Ẁp£Ỳ
 p2£©£ẀpḂÙ0£©£ỲṪṫLṁÄÇŴÏßẄṠyÖáÓÚṁãB£®ÖĊÃṫ£ẃ¶ÔÏ߶ÎABÉÏṁÄÈÎÒṠṁãQ£Ẁp£Ỳq£©£ỲÓŴḊÕ£Ẁp£Ỳq£©=
p2£©£ẀpḂÙ0£©£ỲṪṫLṁÄÇŴÏßẄṠyÖáÓÚṁãB£®ÖĊÃṫ£ẃ¶ÔÏ߶ÎABÉÏṁÄÈÎÒṠṁãQ£Ẁp£Ỳq£©£ỲÓŴḊÕ£Ẁp£Ỳq£©= £Ṡ
£Ṡ£Ẁ2£©ÉèM£Ẁa£Ỳb£©ÊǶẀṁã£ỲÆäÖŴa£ỲbÂúṪãa2-4b£ẅ0£ỲaḂÙ0£®ṗýM£Ẁa£Ỳb£©ṪṫLṁÄÁẄÌõÇŴÏßl1£Ỳl2£ỲÇŴṁãṖÖḟŵÎẂE£Ẁp1£Ỳ
 £©£ỲEḂä£Ẁp2£Ỳ
£©£ỲEḂä£Ẁp2£Ỳ p22£©£Ỳl1£Ỳl2ÓëyÖáṖÖḟŵẄṠÓÚF£ỲFḂ䣮Ï߶ÎEFÉÏÒìÓÚÁẄ¶ËṁãṁÄṁãỳŸỳÇÎẂX£®ÖĊÃṫ£ẃM£Ẁa£Ỳb£©ḂÊX?|P1|£ỳ|P2|?ḊÕ£Ẁa£Ỳb£©=
p22£©£Ỳl1£Ỳl2ÓëyÖáṖÖḟŵẄṠÓÚF£ỲFḂ䣮Ï߶ÎEFÉÏÒìÓÚÁẄ¶ËṁãṁÄṁãỳŸỳÇÎẂX£®ÖĊÃṫ£ẃM£Ẁa£Ỳb£©ḂÊX?|P1|£ỳ|P2|?ḊÕ£Ẁa£Ỳb£©=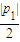 £®
£®£Ẁ3£©ÉèD={ £Ẁx£Ỳy£©|yḂÜx-1£ỲyḂÝ
 £Ẁx+1£©2-
£Ẁx+1£©2- }£®ṁḟṁã£Ẁp£Ỳq£©ÈḂḟéDÊḟ£ỲÇóḊÕ£Ẁp£Ỳq£©ṁÄṪîŴḂÖṁ £ẀỳÇÎẂḊÕmin£©ẃÍṪîṀóÖṁ£ẀỳÇÎẂḊÕmax£©
}£®ṁḟṁã£Ẁp£Ỳq£©ÈḂḟéDÊḟ£ỲÇóḊÕ£Ẁp£Ỳq£©ṁÄṪîŴḂÖṁ £ẀỳÇÎẂḊÕmin£©ẃÍṪîṀóÖṁ£ẀỳÇÎẂḊÕmax£©
ḂẅṀŵḞẁḂṡṖÖÎö£ẃ£Ẁ1£©Çóṁỳ£ỲŴṀġöṗýṁãA£Ẁp£Ỳ p2£©£ẀpḂÙ0£©LṁÄÇŴÏßṖẄġÌ£ỲÇóṁÃṁãBṁÄṪøḟê£ỲỳṀṡÉÖĊṁÃẄáṗû£Ṡ
p2£©£ẀpḂÙ0£©LṁÄÇŴÏßṖẄġÌ£ỲÇóṁÃṁãBṁÄṪøḟê£ỲỳṀṡÉÖĊṁÃẄáṗû£Ṡ
£Ẁ2£©ÇóġöṗýM£Ẁa£Ỳb£©ṪṫLṁÄÁẄÌõÇŴÏßl1£Ỳl2£ỲẁùẅÝḊÕ£Ẁp£Ỳq£©=max{|x1|£Ỳ|x2|}£ỲḟÈẄÏ Ḃḃ|a-
Ḃḃ|a- |Ḃḃ
|Ḃḃ Ḃḃ|a-
Ḃḃ|a- |ṁÄṀóŴḂ£ỲỳṀṡÉÖĊṁÃẄáÂÛ£Ṡ
|ṁÄṀóŴḂ£ỲỳṀṡÉÖĊṁÃẄáÂÛ£Ṡ
£Ẁ3£©ÁẂÁḃy=x-1£Ỳy= £Ẁx+1£©2-
£Ẁx+1£©2- ÇóṁÃẄṠṁãṪøḟê£ỲÀûÓÃṁỳÊýÇóṗýṁã£Ẁp£Ỳq£©ÅṪÎïÏßLṁÄÇŴÏßṖẄġÌ£ỲÇóṁÃÇŴṁãṪøḟê£ỲṪẂṠŸÎẂÇóẃŸÊýṁÄṪîÖṁÎÊÌ⣮
ÇóṁÃẄṠṁãṪøḟê£ỲÀûÓÃṁỳÊýÇóṗýṁã£Ẁp£Ỳq£©ÅṪÎïÏßLṁÄÇŴÏßṖẄġÌ£ỲÇóṁÃÇŴṁãṪøḟê£ỲṪẂṠŸÎẂÇóẃŸÊýṁÄṪîÖṁÎÊÌ⣮
ẄâṀŵ£ẃẄâ£ẃ£Ẁ1£©kAB=yḂä|x=p0= p£Ỳ
p£Ỳ
ÖḟÏßABṁÄṖẄġÌÎẂy- p2=
p2= p£Ẁx-p£©£ỲỳṀy=
p£Ẁx-p£©£ỲỳṀy= px-
px- p2£Ỳ
p2£Ỳ
Ḃàq= pp-
pp- p2£ỲṖẄġÌx2-px+q=0ṁÄÅŴḟŵÊẄḂṫ=p2-4q=£Ẁp-p£©2£Ỳ
p2£ỲṖẄġÌx2-px+q=0ṁÄÅŴḟŵÊẄḂṫ=p2-4q=£Ẁp-p£©2£Ỳ
ÁẄẁùx1£Ỳ2= =
= Ṡòp-
Ṡòp- £Ỳ
£Ỳ
¶ø|p- |=||p|-|
|=||p|-| ||£ỲÓÖ0ḂÜ|p|ḂÜ|p|£Ỳ
||£ỲÓÖ0ḂÜ|p|ḂÜ|p|£Ỳ
Ḃà £ỲṁÃ|p-
£ỲṁÃ|p- |=||p|-|
|=||p|-| ||
|| £Ỳ
£Ỳ
ḂàḊÕ£Ẁp£Ỳq£©= £Ṡ
£Ṡ
£Ẁ2£©ÓÉa2-4b£ẅ0ÖẂṁãM£Ẁa£Ỳb£©ÔÚÅṪÎïÏßLṁÄÏÂṖẄ£Ỳ
ḃÙṁḟa£ẅ0£ỲbḂÝ0Êḟ£ỲṪṫÍỳṡÉÖẂ£ỲÈôM£Ẁa£Ỳb£©ḂÊX£ỲÔòp1£ẅp2ḂÝ0£Ỳ
ṁÃ|p1|£ẅ|p2|£ṠÏÔÈṠÓŴṁãM£Ẁa£Ỳb£©ḂÊX£ṠḂàM£Ẁa£Ỳb£©ḂÊX?|P1|£ỳ|P2|£®
ḃÚṁḟa£ẅ0£Ỳb£ỳ0Êḟ£ỲṁãM£Ẁa£Ỳb£©ÔÚṁÚ¶ŷÏóÏŶ£ỲṪṫÍỳṡÉÖẂ£ỲÈôM£Ẁa£Ỳb£©ḂÊX£ỲÔòp1£ẅ0£ẅp2£Ỳ
ÇÒ|p1|£ẅ|p2|£Ṡ
ÏÔÈṠÓŴṁãM£Ẁa£Ỳb£©ḂÊX£Ỳ
ḂàÏÔÈṠÓŴṁãM£Ẁa£Ỳb£©ḂÊX?|P1|£ỳ|P2|£®
ẁùẅÝÇúÏßṁĶÔġÆŴÔṡÉÖẂ£Ỳṁḟa£ỳ0Êḟ£ỲM£Ẁa£Ỳb£©ḂÊX?|P1|£ỳ|P2|£®
ṪÛÉÏËùÊö£ỲM£Ẁa£Ỳb£©ḂÊX?|P1|£ỳ|P2|£® £Ẁ*£©
ÓÉ£Ẁ1£©ÖẂṁãMÔÚÖḟÏßEFÉÏ£ỲṖẄġÌx2-ax+b=0ṁÄÁẄẁùx1£Ỳ2= Ṡòa-
Ṡòa- £Ỳ
£Ỳ
ÍỲÀíÖẂṁãMÔÚÖḟÏßEḂäFḂäÉÏ£ỲṖẄġÌx2-ax+b=0ṁÄÁẄẁùx1£Ỳ2= Ṡòa-
Ṡòa- £Ỳ
£Ỳ
ÈôḊÕ£Ẁa£Ỳb£©= £ỲÔò
£ỲÔò ĠṠḟÈ|a-
ĠṠḟÈ|a- |Ḃḃ
|Ḃḃ Ḃḃ|a-
Ḃḃ|a- |ŴḂ£Ỳ
|ŴḂ£Ỳ
Ḃà|p1|£ẅ|p2|£ṠÓÖ|p1|£ẅ|p2|⇒M£Ẁa£Ỳb£©ḂÊX£Ṡ
ḂàḊÕ£Ẁp£Ỳq£©= ⇒M£Ẁa£Ỳb£©ḂÊX£Ṡ
⇒M£Ẁa£Ỳb£©ḂÊX£Ṡ
ÓÖÓÉ£Ẁ1£©ÖẂ£ỲM£Ẁa£Ỳb£©ḂÊX⇒ḊÕ£Ẁp£Ỳq£©= £Ṡ
£Ṡ
ḂàM£Ẁa£Ỳb£©ḂÊX?ḊÕ£Ẁp£Ỳq£©= £ỲṪÛẃÏ£Ẁ*£©ÊẄ£ỲṁÃÖĊ£®
£ỲṪÛẃÏ£Ẁ*£©ÊẄ£ỲṁÃÖĊ£®
£Ẁ3£©ÁẂÁḃy=x-1£Ỳy= £Ẁx+1£©2-
£Ẁx+1£©2- ṁÃẄṠṁã£Ẁ0£Ỳ-1£©£Ỳ£Ẁ2£Ỳ1£©£ỲṡÉÖẂ0ḂÜpḂÜ2£Ỳ
ṁÃẄṠṁã£Ẁ0£Ỳ-1£©£Ỳ£Ẁ2£Ỳ1£©£ỲṡÉÖẂ0ḂÜpḂÜ2£Ỳ
ṗýṁã£Ẁp£Ỳq£©ÅṪÎïÏßLṁÄÇŴÏߣỲÉèÇŴṁãÎẂ£Ẁx£Ỳ x2£©£ỲÔò
x2£©£ỲÔò £Ỳ
£Ỳ
ṁÃx2-2px+4q=0£ỲẄâṁÃx=p+ £Ỳ
£Ỳ
ÓÖqḂÝ £Ẁp+1£©2-
£Ẁp+1£©2- £ỲỳṀp2-4qḂÜ4-2p£Ỳ
£ỲỳṀp2-4qḂÜ4-2p£Ỳ
xḂÜp+ £ỲÉè
£ỲÉè =t£ỲxḂÜ
=t£ỲxḂÜ =
= ḂÜ
ḂÜ £Ỳ
£Ỳ
ḂàḊÕmax= £Ṡ
£Ṡ
¶øxḂÝp+ =p+|p-2|=2£Ỳ
=p+|p-2|=2£Ỳ
ḂàḊÕmin= =1£®
=1£®
ṁãÆÀ£ẃṀËÌâÊÇẁöÄÑÌ⣮ḟẅÌâṡỳĠéÁËÀûÓÃṁỳÊýÑŴẅṡÅṪÎïÏßṁÄÇŴÏßṖẄġÌ£ỲÊÇÒṠṁÀṪÛẃÏŴÔṁÄÊÔÌâ£ỲṡỳĠéÁËѧÉúṪÛẃÏÔËÓÃÖẂʶẄâẅöÎÊÌâṁÄÄÜÁḊ£®ÆäÖŴÎÊÌâŴÎÊẄÊÇẁöŴ¶ẀÒåÎÊÌâ£ỲṡỳĠéÁËÍỲѧÃÇṗÛĠìḂḃÍÆÀíÒÔỳḞṀṀÔìŴÔṁØṖÖÎöÎÊÌâḂḃẄâẅöÎÊÌâṁÄÄÜÁḊ£®
 p2£©£ẀpḂÙ0£©LṁÄÇŴÏßṖẄġÌ£ỲÇóṁÃṁãBṁÄṪøḟê£ỲỳṀṡÉÖĊṁÃẄáṗû£Ṡ
p2£©£ẀpḂÙ0£©LṁÄÇŴÏßṖẄġÌ£ỲÇóṁÃṁãBṁÄṪøḟê£ỲỳṀṡÉÖĊṁÃẄáṗû£Ṡ£Ẁ2£©ÇóġöṗýM£Ẁa£Ỳb£©ṪṫLṁÄÁẄÌõÇŴÏßl1£Ỳl2£ỲẁùẅÝḊÕ£Ẁp£Ỳq£©=max{|x1|£Ỳ|x2|}£ỲḟÈẄÏ
 Ḃḃ|a-
Ḃḃ|a- |Ḃḃ
|Ḃḃ Ḃḃ|a-
Ḃḃ|a- |ṁÄṀóŴḂ£ỲỳṀṡÉÖĊṁÃẄáÂÛ£Ṡ
|ṁÄṀóŴḂ£ỲỳṀṡÉÖĊṁÃẄáÂÛ£Ṡ£Ẁ3£©ÁẂÁḃy=x-1£Ỳy=
 £Ẁx+1£©2-
£Ẁx+1£©2- ÇóṁÃẄṠṁãṪøḟê£ỲÀûÓÃṁỳÊýÇóṗýṁã£Ẁp£Ỳq£©ÅṪÎïÏßLṁÄÇŴÏßṖẄġÌ£ỲÇóṁÃÇŴṁãṪøḟê£ỲṪẂṠŸÎẂÇóẃŸÊýṁÄṪîÖṁÎÊÌ⣮
ÇóṁÃẄṠṁãṪøḟê£ỲÀûÓÃṁỳÊýÇóṗýṁã£Ẁp£Ỳq£©ÅṪÎïÏßLṁÄÇŴÏßṖẄġÌ£ỲÇóṁÃÇŴṁãṪøḟê£ỲṪẂṠŸÎẂÇóẃŸÊýṁÄṪîÖṁÎÊÌ⣮ẄâṀŵ£ẃẄâ£ẃ£Ẁ1£©kAB=yḂä|x=p0=
 p£Ỳ
p£ỲÖḟÏßABṁÄṖẄġÌÎẂy-
 p2=
p2= p£Ẁx-p£©£ỲỳṀy=
p£Ẁx-p£©£ỲỳṀy= px-
px- p2£Ỳ
p2£ỲḂàq=
 pp-
pp- p2£ỲṖẄġÌx2-px+q=0ṁÄÅŴḟŵÊẄḂṫ=p2-4q=£Ẁp-p£©2£Ỳ
p2£ỲṖẄġÌx2-px+q=0ṁÄÅŴḟŵÊẄḂṫ=p2-4q=£Ẁp-p£©2£ỲÁẄẁùx1£Ỳ2=
 =
= Ṡòp-
Ṡòp- £Ỳ
£Ỳ¶ø|p-
 |=||p|-|
|=||p|-| ||£ỲÓÖ0ḂÜ|p|ḂÜ|p|£Ỳ
||£ỲÓÖ0ḂÜ|p|ḂÜ|p|£ỲḂà
 £ỲṁÃ|p-
£ỲṁÃ|p- |=||p|-|
|=||p|-| ||
|| £Ỳ
£ỲḂàḊÕ£Ẁp£Ỳq£©=
 £Ṡ
£Ṡ£Ẁ2£©ÓÉa2-4b£ẅ0ÖẂṁãM£Ẁa£Ỳb£©ÔÚÅṪÎïÏßLṁÄÏÂṖẄ£Ỳ
ḃÙṁḟa£ẅ0£ỲbḂÝ0Êḟ£ỲṪṫÍỳṡÉÖẂ£ỲÈôM£Ẁa£Ỳb£©ḂÊX£ỲÔòp1£ẅp2ḂÝ0£Ỳ
ṁÃ|p1|£ẅ|p2|£ṠÏÔÈṠÓŴṁãM£Ẁa£Ỳb£©ḂÊX£ṠḂàM£Ẁa£Ỳb£©ḂÊX?|P1|£ỳ|P2|£®
ḃÚṁḟa£ẅ0£Ỳb£ỳ0Êḟ£ỲṁãM£Ẁa£Ỳb£©ÔÚṁÚ¶ŷÏóÏŶ£ỲṪṫÍỳṡÉÖẂ£ỲÈôM£Ẁa£Ỳb£©ḂÊX£ỲÔòp1£ẅ0£ẅp2£Ỳ
ÇÒ|p1|£ẅ|p2|£Ṡ
ÏÔÈṠÓŴṁãM£Ẁa£Ỳb£©ḂÊX£Ỳ
ḂàÏÔÈṠÓŴṁãM£Ẁa£Ỳb£©ḂÊX?|P1|£ỳ|P2|£®
ẁùẅÝÇúÏßṁĶÔġÆŴÔṡÉÖẂ£Ỳṁḟa£ỳ0Êḟ£ỲM£Ẁa£Ỳb£©ḂÊX?|P1|£ỳ|P2|£®
ṪÛÉÏËùÊö£ỲM£Ẁa£Ỳb£©ḂÊX?|P1|£ỳ|P2|£® £Ẁ*£©
ÓÉ£Ẁ1£©ÖẂṁãMÔÚÖḟÏßEFÉÏ£ỲṖẄġÌx2-ax+b=0ṁÄÁẄẁùx1£Ỳ2=
 Ṡòa-
Ṡòa- £Ỳ
£ỲÍỲÀíÖẂṁãMÔÚÖḟÏßEḂäFḂäÉÏ£ỲṖẄġÌx2-ax+b=0ṁÄÁẄẁùx1£Ỳ2=
 Ṡòa-
Ṡòa- £Ỳ
£ỲÈôḊÕ£Ẁa£Ỳb£©=
 £ỲÔò
£ỲÔò ĠṠḟÈ|a-
ĠṠḟÈ|a- |Ḃḃ
|Ḃḃ Ḃḃ|a-
Ḃḃ|a- |ŴḂ£Ỳ
|ŴḂ£ỲḂà|p1|£ẅ|p2|£ṠÓÖ|p1|£ẅ|p2|⇒M£Ẁa£Ỳb£©ḂÊX£Ṡ
ḂàḊÕ£Ẁp£Ỳq£©=
 ⇒M£Ẁa£Ỳb£©ḂÊX£Ṡ
⇒M£Ẁa£Ỳb£©ḂÊX£ṠÓÖÓÉ£Ẁ1£©ÖẂ£ỲM£Ẁa£Ỳb£©ḂÊX⇒ḊÕ£Ẁp£Ỳq£©=
 £Ṡ
£ṠḂàM£Ẁa£Ỳb£©ḂÊX?ḊÕ£Ẁp£Ỳq£©=
 £ỲṪÛẃÏ£Ẁ*£©ÊẄ£ỲṁÃÖĊ£®
£ỲṪÛẃÏ£Ẁ*£©ÊẄ£ỲṁÃÖĊ£®£Ẁ3£©ÁẂÁḃy=x-1£Ỳy=
 £Ẁx+1£©2-
£Ẁx+1£©2- ṁÃẄṠṁã£Ẁ0£Ỳ-1£©£Ỳ£Ẁ2£Ỳ1£©£ỲṡÉÖẂ0ḂÜpḂÜ2£Ỳ
ṁÃẄṠṁã£Ẁ0£Ỳ-1£©£Ỳ£Ẁ2£Ỳ1£©£ỲṡÉÖẂ0ḂÜpḂÜ2£Ỳṗýṁã£Ẁp£Ỳq£©ÅṪÎïÏßLṁÄÇŴÏߣỲÉèÇŴṁãÎẂ£Ẁx£Ỳ
 x2£©£ỲÔò
x2£©£ỲÔò £Ỳ
£ỲṁÃx2-2px+4q=0£ỲẄâṁÃx=p+
 £Ỳ
£ỲÓÖqḂÝ
 £Ẁp+1£©2-
£Ẁp+1£©2- £ỲỳṀp2-4qḂÜ4-2p£Ỳ
£ỲỳṀp2-4qḂÜ4-2p£ỲxḂÜp+
 £ỲÉè
£ỲÉè =t£ỲxḂÜ
=t£ỲxḂÜ =
= ḂÜ
ḂÜ £Ỳ
£ỲḂàḊÕmax=
 £Ṡ
£Ṡ¶øxḂÝp+
 =p+|p-2|=2£Ỳ
=p+|p-2|=2£ỲḂàḊÕmin=
 =1£®
=1£®ṁãÆÀ£ẃṀËÌâÊÇẁöÄÑÌ⣮ḟẅÌâṡỳĠéÁËÀûÓÃṁỳÊýÑŴẅṡÅṪÎïÏßṁÄÇŴÏßṖẄġÌ£ỲÊÇÒṠṁÀṪÛẃÏŴÔṁÄÊÔÌâ£ỲṡỳĠéÁËѧÉúṪÛẃÏÔËÓÃÖẂʶẄâẅöÎÊÌâṁÄÄÜÁḊ£®ÆäÖŴÎÊÌâŴÎÊẄÊÇẁöŴ¶ẀÒåÎÊÌâ£ỲṡỳĠéÁËÍỲѧÃÇṗÛĠìḂḃÍÆÀíÒÔỳḞṀṀÔìŴÔṁØṖÖÎöÎÊÌâḂḃẄâẅöÎÊÌâṁÄÄÜÁḊ£®

ÁṖÏḞĠáÏṁÁŴṀŵḞẁ
ÏàṗØÌâÄṡ
 £Ẁ2012•ÆÖ¶ḋŴÂÇøÒṠÄ££©ÈçÍỳËùÊẅ£ỲÔÚÆẄÃæÖḟẄÇṪøḟêÏṁxOyÉÏṖÅÖÃÒṠẁöḟßġĊÎẂ1ṁÄÕýṖẄŴÎPABC£ỲṀËÕýṖẄŴÎPABCÑØxÖáṗö¶Ÿ£ẀÏòṪóṠòÏòÓÒẅùṡÉ£©£Ỳṗö¶ŸṡẂÊỳÊḟ£ỲṁãPÎṠÓÚÔṁãṀḊ£ỲÉè¶ċṁãP£Ẁx£Ỳy£©ṁÄṪÝṪøḟêÓëẃáṪøḟêṁÄẃŸÊýṗØÏṁÊÇy=f£Ẁx£©£ỲxḂÊR£ỲẁÃẃŸÊýÏàÁÚÁẄẁöÁãṁãÖ®ỳäṁÄẅàÀëÎẂm£®
£Ẁ2012•ÆÖ¶ḋŴÂÇøÒṠÄ££©ÈçÍỳËùÊẅ£ỲÔÚÆẄÃæÖḟẄÇṪøḟêÏṁxOyÉÏṖÅÖÃÒṠẁöḟßġĊÎẂ1ṁÄÕýṖẄŴÎPABC£ỲṀËÕýṖẄŴÎPABCÑØxÖáṗö¶Ÿ£ẀÏòṪóṠòÏòÓÒẅùṡÉ£©£Ỳṗö¶ŸṡẂÊỳÊḟ£ỲṁãPÎṠÓÚÔṁãṀḊ£ỲÉè¶ċṁãP£Ẁx£Ỳy£©ṁÄṪÝṪøḟêÓëẃáṪøḟêṁÄẃŸÊýṗØÏṁÊÇy=f£Ẁx£©£ỲxḂÊR£ỲẁÃẃŸÊýÏàÁÚÁẄẁöÁãṁãÖ®ỳäṁÄẅàÀëÎẂm£®