题目内容
如图,PA与正方形ABCD中的AD边、AB边都垂直,且2PA=AB.求异面直线AC与PB的夹角.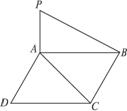
解法一:过D作QD⊥面ABCD且使QD=PA,并设PA=1,连结QA、QC,则QC∥PB.
可求得QC=QA=
,AC=
.
所以cos∠ACQ=
=
.
所以AC与PB的夹角为arccos
.
解法二:以AD为x轴,AB为y轴,AP为z轴,建立坐标系,并设AP=1,
可得
=(2,2,0), 
=(0,2,-1).
cos〈
,
〉=
=
=
,
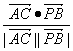
所以AC与PB的夹角为arccos
.
练习册系列答案
阅读快车系列答案
相关题目
如图所示，点P在正方形ABCD所在平面外，PA⊥平面ABCD，PA=AB，则PB与AC所成的角是（ ）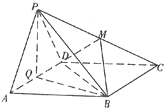
如图边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直，M、Q分别为PC，AD的中点．
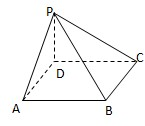如图，在四棱锥P-ABCD中，底面ABCD是边长为的正方形，并且PD=，PA=PC=
如图是一个几何体的平面展开图，其中ABCD为正方形，E、F分别为PA、PD的中点，在此几何体中，给出下面四个结论：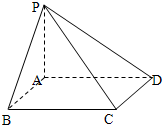
如图四棱锥P-ABCD中，PA⊥底面ABCD，PA=4正方形的边长为2