Question

如图，已知四棱锥P—ABCD，PB⊥AD，侧面PAD为边长等于2的正三角形，底面ABCD为菱形，侧面PAD与底面ABCD所成的二面角为120°.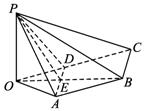

（1）求点P到平面ABCD的距离；

（2）求面APB与面CPB所成二面角的大小.

Answer 1

解:（1）如图，作PO⊥平面ABCD，垂足为点O.连结OB、OA、OD,OB与AD交于点E，连结PE.

∵AD⊥PB,∴AD⊥OB.

∵PA=PD,

∴OA=OD.

    于是OB平分AD，点E为AD的中点，

∴PE⊥AD.

    由此知∠PEB为面PAD与面ABCD所成二面角的平面角，

∴∠PEB=120°,∠PEO=60°.

    由已知可求得PE=，

∴PO=PE·sin60°=×=,

    即点P到平面ABCD的距离为.

（2）如图，取PB的中点G，PC的中点F，连结EG、AG、GF，则AG⊥PB，FG∥BC，FG=BC.

∵AD⊥PB,∴BC⊥PB,FG⊥PB.∴∠AGF是所求二面角的平面角.

∵AD⊥面POB，∴AD⊥EG.

    又∵PE=BE,∴EG⊥PB,且∠PEG=60°.

    在Rt△PEG中，EG=PE·cos60°=.

    在Rt△PEG中，EG=AD=1.

    于是tan∠GAE==.

    又∠AGF=π-∠GAE,∴所求二面角的大小为π-arctan.