题目内容
已知圆C:x2+y2一2x一2y+l=0,直线:y=kx,且与圆C交于P,Q两点,点M(0,b)满足MP⊥MQ.(1)当b=1时,求k的值;
(2)若k>3,求b的取值范围.
【答案】分析:(1)将圆的方程化为标准方程,找出圆心C的坐标与半径,由b=1确定出M的坐标,由MP与MQ垂直得到直线l过圆心,将圆心坐标代入y=kx即可求出k的值;
(2)将圆C的方程与直线l方程联立,消去y得到关于x的一元二次方程,设P(x1,y1),Q(x2,y2),利用根与系数的关系表示出x1+x2与x1x2,由MP与MQ垂直,利用平面向量的数量积运算法则列出关系式,将表示出x1+x2与x1x2代入,整理后得到b+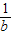 =
=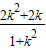 ,设g(k)=
,设g(k)=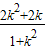 ,求出g(k)的导函数,判断导函数的正负,得到g(k)的单调区间,得到g(k)的范围为b+
,求出g(k)的导函数,判断导函数的正负,得到g(k)的单调区间,得到g(k)的范围为b+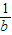 的范围,变形后计算即可得到b的范围.
的范围,变形后计算即可得到b的范围.
解答:解:(1)将圆的方程化为标准方程得:(x-1)2+(y-1)2=1,
当b=1时,点M(0,1)在圆上,
故当且仅当直线l过圆心C时满足MP⊥MQ,
∵圆心坐标为(1,1),
∴将x=1,y=1代入得:k=1;
(2)由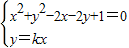 ,
,
消去y,可得(1+k2)x2-2(1+k)x+1=0,
设P(x1,y1),Q(x2,y2),
则x1+x2=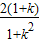 ,x1x2=
,x1x2=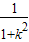 ,
,
由MP⊥MQ,
得到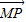 •
•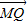 =0,即x1x2+(y1-b)(y2-b)=0,
=0,即x1x2+(y1-b)(y2-b)=0,
又y1=kx1,y2=kx2,
∴x1x2+(kx1-b)(kx2-b)=0,即(1+k2)x1x2-kb(x1+x2)+b2=0,
∴(1+k2)×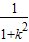 -kb×
-kb×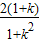 +b2=0,
+b2=0,
当b=0时,此式不成立,从而b+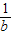 =
=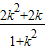 ,
,
令g(k)=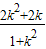 ,则g′(k)=
,则g′(k)=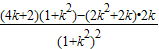 =
=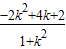 ,
,
设h(k)=-2k2+4k+2,此函数在(3,+∞)上单调递减,即h(k)<h(3)<0,
故g′(k)在(3,+∞)上为负,
∴g(k)=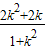 在(3,+∞)上单调递减,即g(k)<g(3)=
在(3,+∞)上单调递减,即g(k)<g(3)=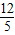 ,
,
且g(k)-2=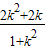 -2=
-2=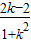 >0,
>0,
∴2<b+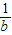 <
<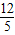 ,
,
则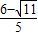 <b<
<b<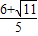 ,且b≠1.
,且b≠1.
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,平面向量的数量积运算法则,韦达定理,研究利用导数研究函数的单调性,是一道综合性较强的试题.
(2)将圆C的方程与直线l方程联立,消去y得到关于x的一元二次方程,设P(x1,y1),Q(x2,y2),利用根与系数的关系表示出x1+x2与x1x2,由MP与MQ垂直,利用平面向量的数量积运算法则列出关系式,将表示出x1+x2与x1x2代入,整理后得到b+
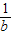 =
=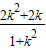 ,设g(k)=
,设g(k)=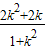 ,求出g(k)的导函数,判断导函数的正负,得到g(k)的单调区间,得到g(k)的范围为b+
,求出g(k)的导函数,判断导函数的正负,得到g(k)的单调区间,得到g(k)的范围为b+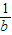 的范围,变形后计算即可得到b的范围.
的范围,变形后计算即可得到b的范围.解答:解:(1)将圆的方程化为标准方程得:(x-1)2+(y-1)2=1,
当b=1时,点M(0,1)在圆上,
故当且仅当直线l过圆心C时满足MP⊥MQ,
∵圆心坐标为(1,1),
∴将x=1,y=1代入得:k=1;
(2)由
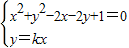 ,
,消去y,可得(1+k2)x2-2(1+k)x+1=0,
设P(x1,y1),Q(x2,y2),
则x1+x2=
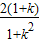 ,x1x2=
,x1x2=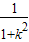 ,
,由MP⊥MQ,
得到
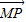 •
•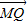 =0,即x1x2+(y1-b)(y2-b)=0,
=0,即x1x2+(y1-b)(y2-b)=0,又y1=kx1,y2=kx2,
∴x1x2+(kx1-b)(kx2-b)=0,即(1+k2)x1x2-kb(x1+x2)+b2=0,
∴(1+k2)×
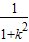 -kb×
-kb×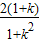 +b2=0,
+b2=0,当b=0时,此式不成立,从而b+
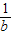 =
=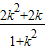 ,
,令g(k)=
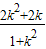 ,则g′(k)=
,则g′(k)=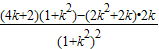 =
=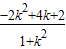 ,
,设h(k)=-2k2+4k+2,此函数在(3,+∞)上单调递减,即h(k)<h(3)<0,
故g′(k)在(3,+∞)上为负,
∴g(k)=
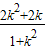 在(3,+∞)上单调递减,即g(k)<g(3)=
在(3,+∞)上单调递减,即g(k)<g(3)=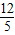 ,
,且g(k)-2=
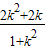 -2=
-2=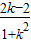 >0,
>0,∴2<b+
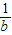 <
<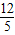 ,
,则
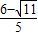 <b<
<b<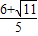 ,且b≠1.
,且b≠1.点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,平面向量的数量积运算法则,韦达定理,研究利用导数研究函数的单调性,是一道综合性较强的试题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 (2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.
(2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.